Question
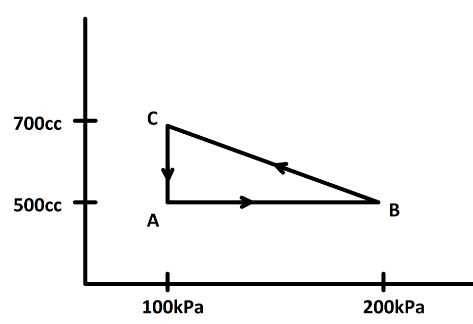
Question: A gas is taken through a cyclic process ABCA as shown in figure. If \[2.4\,cal\] of heat is given in...
A gas is taken through a cyclic process ABCA as shown in figure. If 2.4cal of heat is given in the process. Then, what is the value of J?
Solution
From the second law of thermodynamics, we know that the energy given to a system is used in two ways. One is used to increase the internal energy of the system and the other part is used to do some work done by the system.
Formula used: The second law of thermodynamics is given by,
dQ=dU+dW
where dQ is the energy given to the system dU is the change in internal energy of the system and dW is the work done by the system.
Area of a right angle triangle is, A=21×Base×Height
Complete step by step answer:
We know from the second law of thermodynamics that the work done by a system is the difference between the energy given to the system and the change in internal energy of the system. dQ=dU+dW where dQis the energy given to the system dU is the change in internal energy of the system and dW is the work done by the system.
Now, from the P−V curve we can find the work done by calculating the area under the curve. here we have a cyclic process ABCA. Now, in a cyclic process we know the state of the system does not change. So, change in internal energy is zero. Now, the area under the curve is the difference between the area DBCE and the area DACE or the area of the triangle ABC
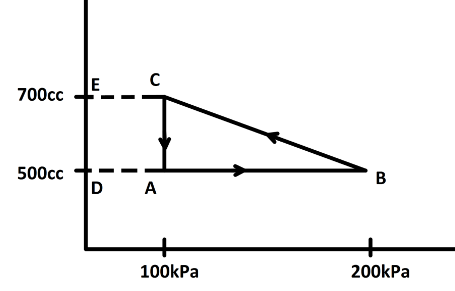
So, the area of triangle ABC will be,
21×(200−100)×103×(700−500)×10−6J [Since, 1cc=10−6m3 and 1kPa=103Pa]
Upon simplifying we have,
area of triangle ABC=21×100×103×200×10−6J
⇒area of triangle ABC=100×100×10−3J
⇒area of triangle ABC=10J
Now, we have given that 2.4calheat is given to the system so, we can write,
2.4J=10 [Since, dU=0]
∴J=2.410=4.166
Hence, the value of J is 4.17J⋅cal−1.
Note: The work done by the system is the area under the P-V curve .Here we have given V-P curve. Also, to find the area under a P-V curve we just integrate as, W=∫PdVWhere, P is a function of Vand T, and dVis the change in volume for a work done dW.
