Question

A gardener presses the grass cutter with a force $F$at an angle $\theta$. Assume the motion of the grasscutter as pure rolling. Find the maximum force $F$ for no relative sliding no relative sliding if the coefficient of friction between the roller and ground is $\mu$.

A. $\dfrac{{\mu mg\cos \theta }}{{\cos \theta + 3\mu \sin \theta }}$
B. $\dfrac{{\mu mg\sin \theta }}{{\cos \theta + 3\mu \sin \theta }}$
C. $\dfrac{{3\mu mg}}{{\cos \theta - 3\mu \sin \theta }}$
D. $\dfrac{{3\mu mg}}{{\cos \theta + 3\mu \sin \theta }}$

Answer 1

We can apply Newton’s Second law of motion to find the maximum force $F$. Newton’s second law of motion states that the summation of all the external forces acting on a body is equal to the product of mass and acceleration.

Complete step by step answer:
We can refer to the figure below:

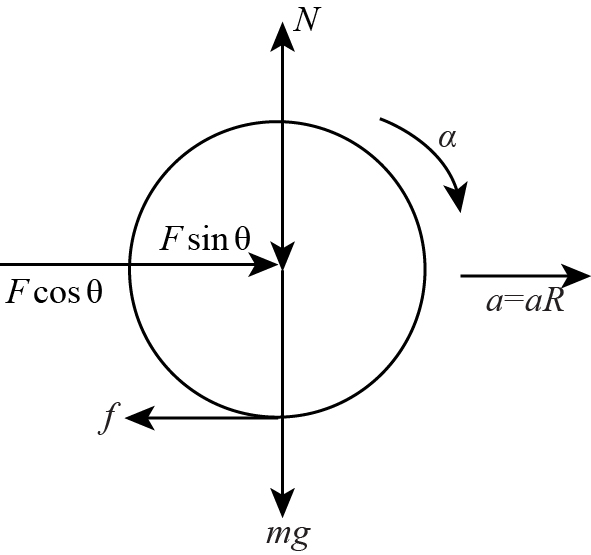
In this above FBD, the roller is moving in the positive forward direction and $a$ is the acceleration of the roller. Apart from it, it has $F\cos \theta$ and $F\sin \theta$ are the horizontal and vertical components of the applied force F. $f$ is the frictional force between ground and roller, and mg is the weight of roller acting downwards which is balanced by the normal reaction N.
We will, therefore, apply Newton's second law of motion.
$\Rightarrow F\cos \theta - f = ma$ …………….…… (i).
Here $F$ is the applied force, $f$ is the frictional force and $a$ is the acceleration of the center of mass, $m$ is the mass of the grass cutter.
Therefore, write the equation of torque.
$\Rightarrow fR = I\alpha$ ………………..…… (ii)
Here $I = \dfrac{1}{2}m{R^2}$ and $\alpha = \dfrac{a}{R}$ for the pure rolling condition.
We will now substitute the value of $I$ and $\alpha$ in equation (ii) and it comes out to be,
$\Rightarrow f = \dfrac{{ma}}{2}$
$\therefore ma = 2f$ ………………..…… (iii)
We will now substitute equation (iii) in equation (i) and it comes out as,
$\Rightarrow f = \dfrac{{F\cos \theta }}{3}$ ………………...…… (iv)
We will apply static equilibrium of forces in Y direction.
$N = F\sin \theta + mg$ ………………...… (v)
Here, $N$ is the normal reaction.
We will now apply the law of friction, it comes out to be,
$f \le \mu N$ …………………... (vi)
We can substitute $f = \dfrac{{F\cos \theta }}{3}$ and $N = F\sin \theta + mg$ to find the value of F. Hence it becomes,
$\Rightarrow \dfrac{F \cos \theta}{3} \le\, \mu$($mg+F\sin \theta$)
$\Rightarrow F \le \dfrac{{3\mu mg}}{{\cos \theta - 3\mu \sin \theta }}$

Hence the correct option is (C).

Note:
In the question the roller moves without slipping following the pure rolling condition. There is no relative sliding. Here, although the roller is moving forward the direction of friction is opposite to the direction of the roller as the lower end of the roller has the motion on the opposite side.