Question

A galvanometer with a resistance $100\Omega$ gives a full scale deflection with a current of 10mA. The value of shunt, in order to convert it into an ammeter of 10 ampere range will be
a) $-10\Omega$
b)$1\Omega$
c)$0.1\Omega$
d)$0.01\Omega$

Answer 1

In the question it is asked that a galvanometer of resistance $100\Omega$ is to be converted into an ammeter of range 10A. In order to convert a galvanometer into an ammeter, we connect a resistance in parallel with the galvanometer. Hence using Kirchhoff's voltage law we can determine the shunt required in parallel.
Formula used:
$S=\dfrac{{{I}_{g}}G}{I-{{I}_{g}}}$

Complete answer:

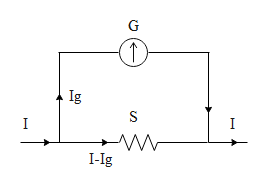
Let us say we have a galvanometer of resistance ‘G’ which is to be converted into an ammeter which can measure the current up to ‘I’ ampere in the circuit. Galvanometer is very flexible and gives full scale deflection for even small values of current. Therefore we need to connect a resistance ‘S ’in parallel with the galvanometer so that all the current goes into the shunt and the galvanometer can read the current in the circuit to a greater extent.
Let us say the potential difference across the galvanometer be ${{V}_{G}}$ and that of the shunt be ${{V}_{S}}$ .In the above figure if we apply Kirchhoff’s law to the closed loop we get,
$\begin{aligned} & {{V}_{G}}-{{V}_{S}}=0 \\\ & \therefore {{V}_{G}}={{V}_{S}} \\\ \end{aligned}$
Let us say the current for which the galvanometer gives full scale deflection is ${{I}_{g}}$ and the range of current which we want to measure is ‘I’. From ohms law the equation 1 can be written as,
$\begin{aligned} & {{V}_{G}}={{V}_{S}} \\\ & \Rightarrow G{{I}_{g}}=S(I-{{I}_{g}}) \\\ & \Rightarrow S=\dfrac{G{{I}_{g}}}{(I-{{I}_{g}})} \\\ & \because G=100\Omega ,\text{ }I=10A\text{ }{{I}_{g}}=10mA \\\ & \Rightarrow S=\dfrac{100\times 10mA}{(10-10mA)}=\dfrac{1}{9.99}\Omega \\\ & \therefore S=0.1\Omega \\\ \end{aligned}$

Therefore the correct answer of the above question is option c.

Note:
The ohm's law states that the current flowing through the wire is proportional to the potential difference and the constant of proportionality is the resistance of the wire. Smaller the resistance greater will be the ability of the galvanometer to detect current. This is because as the resistance becomes smaller more current will flow through the shunt.