Question

A galvanometer when shunted with a resistance of $2.5\,\Omega$ gives a full-scale deflection for $5\,{\text{A}}$ . When it is connected in series with a resistance of $140\,\Omega$ , it gives a full-scale deflection for $150$ volt. Compute the resistance of the galvanometer.

Answer 1

First of all, we will draw the circuit diagrams for both the series and parallel connection. Then we will build up two equations from the two diagrams. In series, the sum of potential differences of each element is equal to the potential difference of the whole circuit. In parallel, voltage remains the same. Substitute the required values and manipulate accordingly.

Complete step by step answer:
First case,
In the given question, following data are supplied:
A galvanometer is shunted with a resistance of $2.5\,\Omega$ .
Shunting means to connect the galvanometer in parallel with the shunt resistor.
It gives a full-scale deflection when the total current flowing through the circuit is $5\,{\text{A}}$ .
In the case of parallel connection, some amount of current will flow through the galvanometer while the rest will flow through the shunt resistor.
For this we draw the circuit, to have better understanding.

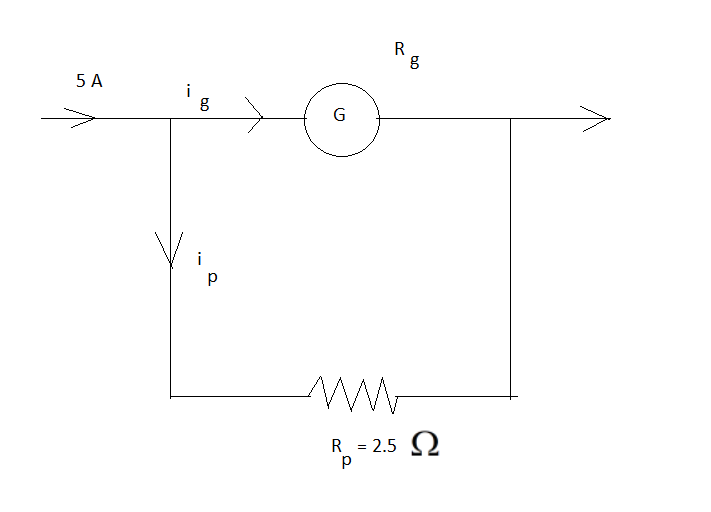
In the figure,
${i_g}$ indicates current flowing through the galvanometer.
${R_g}$ indicates resistance of the galvanometer.
${i_p}$ indicates the current flowing through the shunt resistor.
${R_p}$ indicates the resistance of the shunt resistor.

We can write:
${i_g} + {i_p} = 5$
${i_g} = \left( {\dfrac{{{R_p}}}{{{R_g} + {R_p}}}} \right) \times 5$ …… (1)

Second case,
The resistor which is connected in series with the galvanometer is $140\,\Omega$ and the potential difference at which the galvanometer gives is $150$ volt.
For this we draw the circuit, to have better understanding.

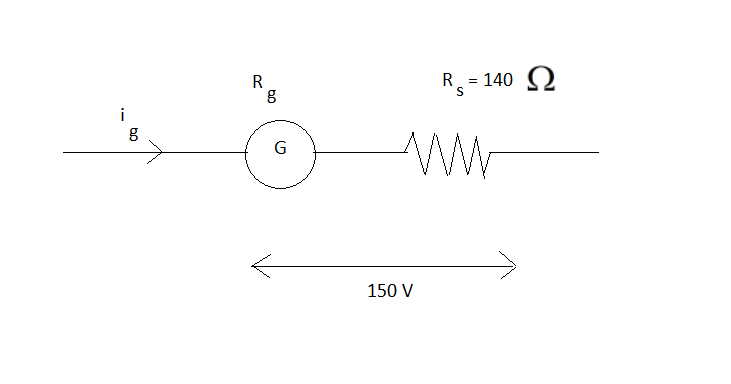
${i_g}$ indicates current flowing through the galvanometer and the resistor.
${R_g}$ indicates resistance of the galvanometer.
${R_s}$ indicates the resistance of the resistor in series.

We can write:
{i_g}{R_g} + {i_g}{R_s} = 150 \\\
\implies {i_g}\left( {{R_g} + {R_s}} \right) = 150 \\\
$\implies {i_g} = \dfrac{{150}}{{{R_g} + {R_s}}}$ …… (2)

Now, we equate the equations (1) and (2),
$\left( {\dfrac{{{R_p}}}{{{R_g} + {R_p}}}} \right) \times 5 = \dfrac{{150}}{{{R_g} + {R_s}}}$ …… (3)
Substituting the required values in the equation (3), we get:
\left( {\dfrac{{2.5}}{{{R_g} + 2.5}}} \right) \times 5 = \dfrac{{150}}{{{R_g} + 140}} \\\
\implies \dfrac{{12.5}}{{{R_g} + 2.5}} = \dfrac{{150}}{{{R_g} + 140}} \\\
\implies \dfrac{{{R_g} + 140}}{{{R_g} + 2.5}} = \dfrac{{150}}{{12.5}} \\\
\implies \dfrac{{{R_g} + 140}}{{{R_g} + 2.5}} = 12 \\\
Again, simplifying further, we get:
{R_g} + 140 = 12\left( {{R_g} + 2.5} \right) \\\
11{R_g} = 110 \\\
{R_g} = 10\,\Omega \\\
Hence, the resistance of the galvanometer is $10\,\Omega$ .

Note:
It is important to note that, in case of series connection, the current flowing through all the elements is the same, whereas in case of parallel connection, the potential difference across all the elements are equal.