Question

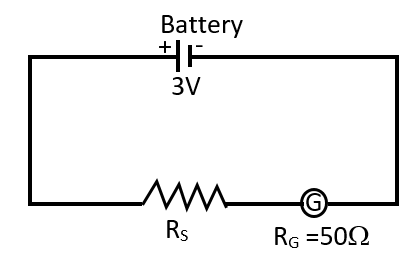
A galvanometer of resistance $50\Omega$ is connected to a battery of 3V along with a resistance of $2950\Omega$ in series. A full scale deflection of 30 divisions is obtained in the galvanometer. In order to reduce this deflection to 20 divisions the resistance in series should be:
A. 4450\Omega \\\ B. 5050\Omega \\\ C. 5550\Omega \\\ D. 6050\Omega \\\

Answer 1

We have to calculate current at full scale, then we have to calculate resistance needed for $\dfrac{2}{3}rd$ of current.

Complete step by step answer:
Given values are {R_G} = 50\Omega \\\ V = 3Volts \\\ {R_{{s_1}}} = 2950\Omega \\\ {Ohm’s Law: V$=$IR}
Case (i)Current in this case is
{I_1} = \dfrac{V}{{{R_1}}} \\\ = \dfrac{3}{{2950 + 50}} \\\ = \dfrac{3}{{3000}}A \\\ {I_1} = \dfrac{1}{{1000}}A \\\
At this current, there is full scale deflection of 30 divisions in the galvanometer. Now in the second case, deflection is only 20 divisions which means deflection is $\dfrac{2}{3}rd$ of the previous case. Hence current will also be $\dfrac{2}{3}rd$ in this case.

Case (ii)
So,
${I_2} = \dfrac{2}{3}\left[ {\dfrac{1}{{1000}}} \right]A$
$V = {I_2}\,{R_2}$
$So,\,\,{R_2} = \dfrac{v}{{{I_2}}}$
${R_2} = \dfrac{3}{2} \times 3000$
$\implies {R_2} = \dfrac{{9000}}{2} = 4500$
Now,
${R_2} = {R_{{s_2}}} + {R_G}$
$\implies {R_{{s_2}}} = 4500 - 50$

So, the correct answer is “Option A”.

Note: 1. Galvanometer gives full scale deflection when maximum limit current flows through it.
2. Total resistance of the given circuit is sum of resistance of galvanometer and the series resistance. So do not think that total resistance ${{\text{R}}_{{\text{2 = }}}}{\text{4500}}\Omega$ is the answer. Subtract the galvanometer from it to get the correct answer.