Solveeit Logo
Login

Question

Question: A galvanometer of resistance \(100\,\Omega \)gives a full-scale deflection for a current of \({10^{ ...

A galvanometer of resistance 100 Ω100\,\Omega gives a full-scale deflection for a current of 10−5 A{10^{ - 5}}\,A . To convert it into an ammeter capable of measuring up to 1 A, we should connect a resistance of
A. 1 Ω1\,\Omega in parallel
B. 10−3 Ω{10^{ - 3}}\,\Omega in parallel
C. 105 Ω{10^5}\,\Omega in parallel
D. 100 Ω100\,\Omega in parallel

Explanation

Solution

We will first calculate the current distributions in the circuit and then apply the basic fundamentals of a series and parallel combination. In a parallel combination, the total current flowing in the circuit is the sum of the individual currents flowing in each arm of the connection. We will then calculate the supply voltage and substitute the known values in the equation to get the answer.

Complete answer:
Let’s first draw the circuit diagram to help understand the concept better.

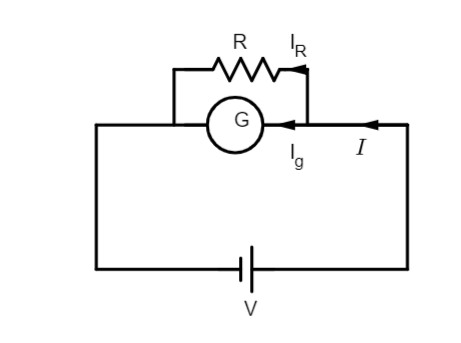
Here V is the source voltage, I is the total current flowing in the circuit, IG{I_G} is the current flowing through the galvanometer and IR{I_R} is the current flowing through the external resistance applied to extend the range of the ammeter.
We can see that I=IG+IRI = {I_G} + {I_R}
Since the combination of the galvanometer and the external resistance is parallel, the voltage drop across each element is the same and equal to the source voltage.
So, the above equation can be rewritten as
I=VR+VG           .........(1)I = \dfrac{V}{R} + \dfrac{V}{G}\,\,\,\,\,\,\,\,\,\,\,.........(1) where R and G are the resistances of the external resistor and galvanometer respectively.
Now, when the external resistor was not applied, the galvanometer offered the resistance. The voltage from the source can be calculated.
V=I′GV = {I'}G where I′{I'} is the current in the circuit when no external resistor is connected.
Substituting the values,
V=100×10−5 VV = 100 \times {10^{ - 5}}\,V
⇒V=10−3 V\Rightarrow V = {10^{ - 3}}\,V
Substituting all the known values in equation 1 we get,
1=10−3(1R+1100) 1 = {10^{ - 3}}(\dfrac{1}{R} + \dfrac{1}{{100}})\,
1R+1100=1000\dfrac{1}{R} + \dfrac{1}{{100}} = 1000
Further solving this equation, we get,
1R=1000−0.01\dfrac{1}{R} = 1000 - 0.01
⇒R=0.001 Ω\Rightarrow R = 0.001\,\Omega
∴R=10−3 Ω\therefore R = {10^{ - 3}}\,\Omega
Hence, option B is the correct answer.

Note:
A galvanometer’s current sensitivity is determined by the amount of electric current required by the meter's coil to produce the required deflection. The smaller the amount of current required to produce the required deflection, the greater the sensitivity of the meter. It is designed to carry the majority of the circuit current so that only a small portion of it flows through it.