Question

A galvanometer of resistance $100$ ohm gives full scale deflection with $5$ milliampere current. To convert it into a $5$ volt range voltmeter, the value of resistance connected in series is:
(A) $900\Omega$
(B) $9999\Omega$
(C) $10000\Omega$
(D) $1{\text{M}}\Omega$

Answer 1

Hint : To solve this question, we have to use the value of the full scale deflection current given in the question when the voltmeter shows the maximum voltage. Then by calculating the drop across the voltmeter in terms of the unknown resistance and equating it with the maximum voltage we will get the final answer.

Complete step by step answer
Let the value of the resistance required to be connected in series with the galvanometer be $R$ , as shown in the figure below.

After connecting this resistance in series with the galvanometer, the galvanometer gets converted into a $5$ volt range voltmeter. This means that the value “ $5$ volt” is the maximum value that this voltmeter can measure. So when the potential difference across the voltmeter becomes equal to $5$ volt then the galvanometer will show full scale deflection. According to the question, the galvanometer gives the full scale deflection for a current equal to $5$ milliampere. Therefore when the voltage across the voltmeter is equal to $5$ volts, then a current of $5$ milliampere will flow through it. This is as shown in the below diagram.

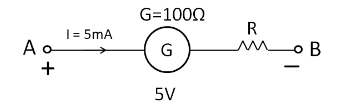
From the above figure we have
${V_A} - {V_B} = 5{\text{V}}$
$\Rightarrow 5{\text{mA}}\left( {100 + R} \right) = 5{\text{V}}$
We know that $1{\text{mA}} = {10^{ - 3}}{\text{A}}$ . So we have
$5 \times {10^{ - 3}}\left( {100 + R} \right) = 5$
$\Rightarrow \left( {100 + R} \right) = 1000$
Subtracting $100$ from both the sides, we finally get
$R = 900\Omega$
Thus, the value of resistance connected in series with the galvanometer to convert it into a $5$ volt range voltmeter is equal to $900\Omega$ .
Hence, the correct answer is option A.

Note
There should not be the misconception that the entire voltage appears across the galvanometer only. In fact almost all the voltage appears on the series resistance. This is done to take care of the fact that the galvanometer is a very sensitive device so very little fraction of the voltage should appear across it.