Question

A galvanometer of $100\Omega$ resistance gives full scale deflection with 0.01A current. How much resistance should be connected to convert it into an ammeter of range 10A?
A. 0.1 in parallel
B. 0.1 in series
C. 0.2 in parallel
D. 0.2 in series

Answer 1

The connection and value of the shunt resistance should be made such that most of the current passes through the shunt. Recall that, in order to convert a galvanometer to ammeter, shunt should be connected in parallel. Clearly, the voltage is the same across both of them. Applying Ohm’s law we get the voltage in terms of current and resistance. Also, substitute for current across shunt using Kirchoff’s junction rule and hence find the shunt resistance.

Formula used:
Ohm's law,
V=IR
Kirchoff’s junction rule,
$I={{I}_{G}}+{{I}_{S}}$

Complete step-by-step answer:
We know that, Galvanometer is a device that is used to detect current of very small current in a circuit. It basically consists of a coil pivoted between concave pole faces of a strong laminated horse shoe magnet. This coil shows deflection when current passes through it. Also, the deflection is directly proportional to the amount of current passing through the coil. We should note here that the galvanometer coil has a moderate resistance of 100ohms and by itself it has a small current carrying capacity.
We use an ammeter to measure large electric currents in circuits. Normally, we connect an ammeter in series within a circuit.
Now that we know a bit about galvanometer and ammeter, let us look into converting a galvanometer in ammeter. A galvanometer by itself can only detect small currents, but by converting it into ammeter, it can measure large currents. This conversion is done by connecting a low resistance in parallel with the galvanometer. We call this low resistance ‘shunt resistance’. Shunt resistance’s value is adjusted such that most of the current passes through the shunt.
Let the resistance of galvanometer be represented by ${{R}_{G}}$ and let the current at which the galvanometer show full-scale deflection be, ‘${{I}_{G}}$’. Then, voltage across the galvanometer is given by,
$V={{I}_{G}}{{R}_{G}}$ ……………….. (1)
But we are given ${{I}_{G}}$ and ${{R}_{G}}$ in the question as,
${{I}_{G}}=0.01A$
${{R}_{G}}=100\Omega$
Equation (1) now becomes,
$V=0.01\times 100=1V$ ………………… (2)
By Kirchoff’s junction rule, current entering the junction is equal to the current leaving the junction.

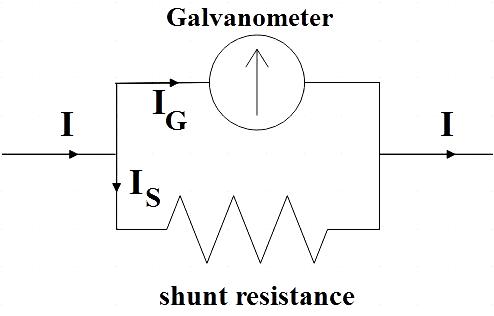
$I={{I}_{G}}+{{I}_{S}}$
${{I}_{S}}=I-{{I}_{G}}$ ………………… (3)
Voltage across shunt resistance,
$V={{I}_{S}}{{R}_{S}}$ …………………… (4)
Substituting (3) in (4), we get,
$V=\left( I-{{I}_{G}} \right){{R}_{S}}$ …………………. (5)
Since the connection is in parallel, the voltage across galvanometer and shunt is the same, so, we can equate (5) to (2),
$\left( I-{{I}_{G}} \right){{R}_{S}}=1V$ ………………….. (6)
‘$I$’ is given as 10A in the question, so,
${{R}_{S}}=\dfrac{1}{\left( 10-0.01 \right)}=\dfrac{1}{9.99}=0.1\Omega$
So, resistance of $0.1\Omega$ should be connected in parallel to convert the given galvanometer into an ammeter of range 10A.

So, the correct answer is “Option A”.

Note: You shouldn't by-heart the formulae for shunt resistance used to convert the galvanometer into ammeter. All you have to remember is that the shunt is connected in parallel with the galvanometer to convert it into ammeter and you could derive the formula from there. You could also convert a galvanometer into voltmeter by connecting a high resistance in series with it.