Question

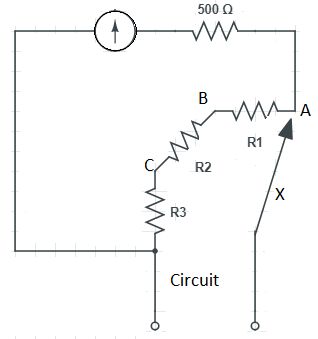
A galvanometer is used to measure the small currents. A certain galvanometer has a resistance of 500Ω and gives a full scale deflection for a current of 200μA. This meter is connected as shown in the figure to make a multi range current meter. Connections to the circuit are made at the terminal shown. The currents in the external circuit needed to give full scale deflection when X is connected to A, B and C in turn is shown in the table.

X connected to	Current in the external circuit (mA)
A	1
B	10
C	100

Find out the of ${{R}_{3}}$is

A. 2.25 Ω
B. 0.25 Ω
C. 1.25 Ω
D. 3.25Ω

Answer 1

In order to solve this question we have to use the Kirchhoff’s law for the give 3 conditions one by one which will give us combination of resistance by solving those equation we will get value of resistance ${{R}_{3}}$.

Formula used:
V=IR

Complete step by step solution:
Now in order to get the solution we have to apply given 3 conditions one by one.
Given data:
$\begin{aligned} & R=500\Omega \\\ & I=200\mu A \\\ & =200\times {{10}^{-6}}A \\\ & {{I}_{1}}=1mA \\\ & =1\times {{10}^{-3}}A \\\ & {{I}_{2}}=10mA \\\ & =10\times {{10}^{-3}}A \\\ & {{I}_{3}}=100mA \\\ & =100\times {{10}^{-3}} \\\ \end{aligned}$

Now condition (i) when X is connected to A.

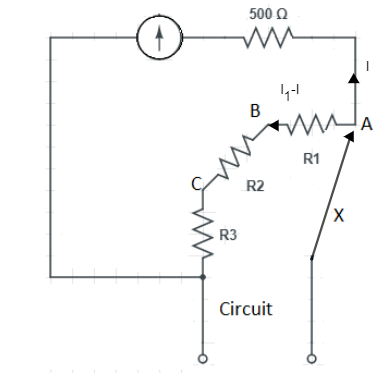
Now from the fig (i) let’s apply Kirchhoff’s law
$500\times I=\left( {{R}_{1}}+{{R}_{2}}+{{R}_{3}} \right)\times \left( {{I}_{1}}-I \right)$

Here all the three resistance are connected in the series therefore we can apply the series rule of the resistance.

Now let’s substitute all the values in the equation.
$\begin{aligned} & \Rightarrow 500\times 200\times {{10}^{-6}}=\left( {{R}_{1}}+{{R}_{2}}+{{R}_{3}} \right)\times \left( 1\times {{10}^{-3}}-200\times {{10}^{-6}} \right) \\\ & \Rightarrow {{R}_{1}}+{{R}_{2}}+{{R}_{3}}=\dfrac{500\times 200\times {{10}^{-6}}}{0.8\times {{10}^{-3}}} \\\ & \Rightarrow {{R}_{1}}+{{R}_{2}}+{{R}_{3}}=\dfrac{10\times {{10}^{4}}\times {{10}^{-6}}\times {{10}^{3}}}{0.8} \\\ & \Rightarrow {{R}_{1}}+{{R}_{2}}+{{R}_{3}}=125 \\\ & \therefore {{R}_{1}}+{{R}_{2}}=125-{{R}_{3}}....\left( 1 \right) \\\ \end{aligned}$

Now let’s apply the second condition:
When X is connected to the point B, circuit will becomes as shown in the figure (i)

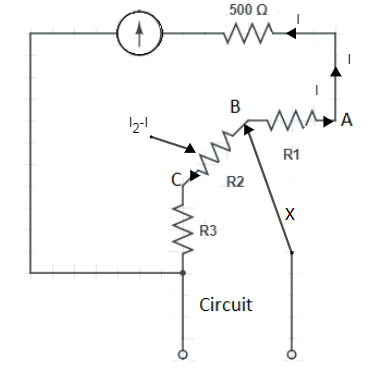
Now let’s apply Kirchhoff’s law in the circuit shown in the figure (ii)

& \Rightarrow \left( 500+{{R}_{1}} \right)I=\left( {{R}_{2}}+{{R}_{3}} \right)\times \left( {{I}_{2}}-I \right) \\\ & \Rightarrow \left( 500+{{R}_{1}} \right)\times 200\times {{10}^{-6}}=\left( {{R}_{2}}+{{R}_{3}} \right)\times \left( 10\times {{10}^{-3}}-200\times {{10}^{-6}} \right) \\\ & \Rightarrow \left( 500+{{R}_{1}} \right)=\dfrac{\left( {{R}_{2}}+{{R}_{3}} \right)\times 9.8\times {{10}^{-3}}}{200\times {{10}^{-6}}} \\\ & \therefore \left( 500+{{R}_{1}} \right)=49\left( {{R}_{2}}+{{R}_{3}} \right)....\left( 2 \right) \\\ \end{aligned}$$ Now let’s apply third condition: When X is connected to the point C our circuit will be, 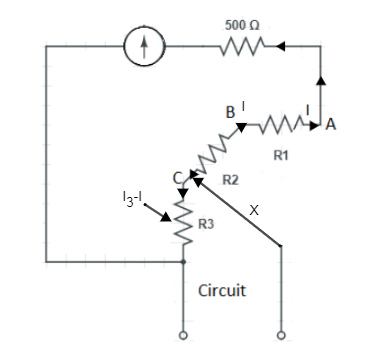 Now let’s apply Kirchhoff’s law on circuit shown in the figure (iii) $\begin{aligned} & \Rightarrow \left( 500+{{R}_{1}}+{{R}_{2}} \right)\times I={{R}_{3}}\times \left( {{I}_{3}}-I \right) \\\ & \Rightarrow \left( 500+{{R}_{1}}+{{R}_{2}} \right)\times 200\times {{10}^{-6}}={{R}_{3}}\left( 100\times {{10}^{-3}}-200\times {{10}^{-6}} \right) \\\ & \Rightarrow 500+{{R}_{1}}+{{R}_{2}}=\dfrac{{{R}_{3}}\times 99.8\times {{10}^{-3}}}{200\times {{10}^{-6}}} \\\ & \therefore 500+{{R}_{1}}+{{R}_{2}}={{R}_{3}}\times 499...\left( 3 \right) \\\ \end{aligned}$ Now from the equation (1) substitute value of the $\left( {{R}_{1}}+{{R}_{2}} \right)$ in the equation (3) $\begin{aligned} & \Rightarrow 500+125-{{R}_{3}}=499{{R}_{3}} \\\ & \Rightarrow 00{{R}_{3}}=625 \\\ & \therefore {{R}_{3}}=1.25\Omega \\\ \end{aligned}$ **Hence, the option (c) is correct.** **Note:** When we are dividing current be careful when putting $\left( {{I}_{1}}-I \right)$ or $\left( {{I}_{2}}-I \right)$ or $\left( {{I}_{3}}-I \right)$ it can be mistaken or misplaced as $\left( I-{{I}_{1}} \right)$ or $\left( I-{{I}_{2}} \right)$ or $\left( I-{{I}_{3}} \right)$ which can lead us to the wrong answer.