Question

A galvanometer has a current range of $15mA$ and voltage range $750mV$. To convert this galvanometer into an ammeter of range $25A$, the required shunt is
$A)\text{ }0.8\Omega$
$B)\text{ }0.93\Omega$
$C)\text{ }0.03\Omega$
$D)\text{ }2.0\Omega$

Answer 1

Hint: A galvanometer is converted to an ammeter by connecting a very small resistance (shunt) in parallel. This increases the current range of the whole setup a lot of current passes through the shunt. By using the formula for the distribution of current in two parallel branches, we can get the required equation for the resistance of the shunt.

Formula used:
$V=IR$

Complete step by step answer:
It is given that the current range of the galvanometer is ${{I}_{G}}=15mA=15\times {{10}^{-3}}A$ $\left( \because 1mA={{10}^{-3}}A \right)$
It is also given that the voltage range of the galvanometer is ${{V}_{G}}=750mV=750\times {{10}^{-3}}V$ $\left( \because 1mV={{10}^{-3}}V \right)$
Let the resistance of the galvanometer be $G$.
Now, according to Ohm’s law the current $I$ passing through a resistor of resistance $R$ is related to the voltage $V$ across it by
$V=IR$ --(1)
Therefore, using (1), we get,
${{V}_{G}}={{I}_{G}}G$
$\therefore G=\dfrac{{{V}_{G}}}{{{I}_{G}}}=\dfrac{750\times {{10}^{-3}}}{15\times {{10}^{3}}}=50\Omega$
Hence, the resistance of the galvanometer is $50\Omega$.
Now, to convert it into an ammeter, a very small shunt resistance has to be connected in parallel. This increases the current range of this setup. This is because in absence of the shunt, a maximum current of ${{I}_{G}}$ could enter the galvanometer. However, when a shunt is connected in parallel to form an ammeter setup, a large current will enter the setup, ${{I}_{G}}$ current will flow in the branch of the galvanometer while the rest of the current can flow through the shunt.
Hence, let us connect a shunt of resistance $S$ in parallel.
Let the total current entering the ammeter setup be $I$.

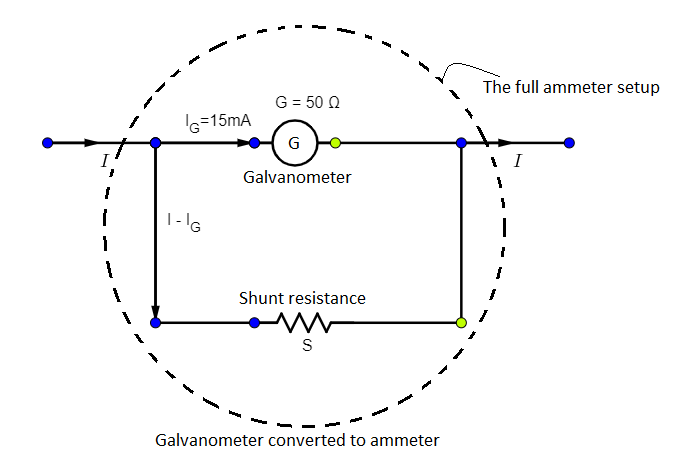
Now, the current entering in the branch of the galvanometer is given by
${{I}_{G}}=\dfrac{S}{G+S}I$ ($\because$ From Ohm’s law, we see $I\propto \dfrac{1}{R}$)
Now according to the question $I=25A$.
Therefore putting this value, we get,
$15\times {{10}^{-3}}=\dfrac{S}{50+S}25$
$\Rightarrow 0.015\left( 50+S \right)=25S$
$\Rightarrow \left( 0.015\times 50 \right)+0.015S=25S$
$\Rightarrow 0.75=25S-0.015S=24.985S$
$\Rightarrow S=\dfrac{0.75}{24.985}=0.03\Omega$
Hence, the required resistance of the shunt is $0.03\Omega$.
Therefore, the correct option is $C)\text{ }0.03\Omega$.

Note: Students must remember that to convert a galvanometer into an ammeter, a very small shunt resistance has to be attached in parallel always. This increases the current range (which is required for an ammeter, as an ammeter measures current). On the other hand, to convert the galvanometer into a voltmeter, a large resistance has to be connected in series. This increases the voltage range of the whole setup as a lot of the voltage drop is across the large resistance. This is required for a voltmeter as it measures the voltage drop.
Students must also not forget to find out the galvanometer resistance. The galvanometer resistance can be considered to be a simple resistance that is in series with an ideal galvanometer (having zero resistance).