Question

A galvanometer has a coil resistance of $100\Omega$. It gives a full-scale deflection when a current of 0.001A is passed through it. The value of resistance which can convert the galvanometer into an ammeter giving full-scale deflection for a current of 10A is:
A. ${10^{ - 4}}\Omega$
B. ${10^{ - 2}}\Omega$
C. ${10^4}\Omega$
D. ${10^2}\Omega$

Answer 1

The galvanometer can be converted into an ammeter by a process called shunting. Shunting is the process of connecting another resistance in parallel with the main resistance.

Complete Step by Step Answer:
A galvanometer is very helpful in converting it to an ammeter and voltmeter to measure the current and voltage in the circuit respectively.
Even though the galvanometer shows the direction of the current flowing, it cannot be used to measure currents since the full-scale deflection of the galvanometer is in a few $\mu A$. Hence, an additional attachment has to be made to convert a galvanometer into a full-fledged ammeter of several ranges starting from $mA$ to A.
A galvanometer is converted to an ammeter by connecting a resistor parallel to it, known as shunt resistance.
Here is a circuit to convert a galvanometer into an ammeter.

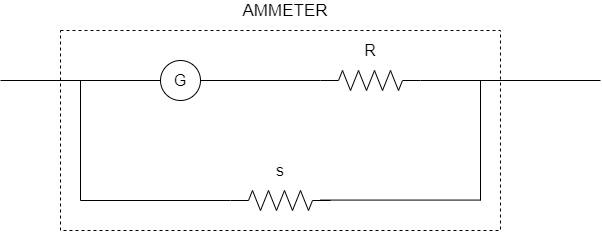
The galvanometer is represented by G and R is the resistance of the galvanometer. Here, S is called the shunt resistance, which is connected in parallel to the galvanometer.
The shunt resistance to be connected to convert to an ammeter of highest range $I$, is given by –
$S = \dfrac{{R{I_g}}}{{I - {I_g}}}$
where ${I_g}$ is the full-scale deflection current of the galvanometer.
Given,
Resistance of the galvanometer coil, $R = 100\Omega$
Full-scale deflection current, ${I_g} = 0.001A$
Required range of current, 0 – 10A $\to I = 10A$
Substituting in the above equation, we get the shunt resistance –
$S = \dfrac{{100 \times 0.001}}{{10 - 0.001}}$
On simplification,
$S = \dfrac{{0.1}}{{9.999}} = 0.0100001\Omega = {10^{ - 2}}\Omega$

$\therefore$ The value of resistance is ${10^{ - 2}}\Omega$. Hence, option (B) is the correct answer.

Note:
You have to always make a note that the shunt resistance is a very small value of resistance. If you get a higher number than the resistance of the galvanometer itself, you are definitely in the wrong direction. Conversely, if you are converting a galvanometer into a voltmeter, the resistance connected in series should be a really high value of resistance. If you get a lower number than the galvanometer resistance, you are definitely wrong there, too.