Question
Question: A galvanometer gives full scale deflection with 0.006 A current. By connecting it to a \[4990\,\Omeg...
A galvanometer gives full scale deflection with 0.006 A current. By connecting it to a 4990Ω resistance, it can be converted into a voltmeter of range 0-30 V. If connected to a 2492nΩ resistance, it becomes an ammeter of range 0-1.5 A. The value of n is:
Solution
When the external resistance is connected in series with the galvanometer, the galvanometer works as voltmeter. When the external shunt resistance is connected across the galvanometer, it acts as the ammeter. The potential drop across the parallel circuit remains the same.
Formula used:
Ohm’s law, V=IR,
where, V is the voltage, I is the current and R is the resistance.
Complete step by step answer:
When we connect an external resistance series with a galvanometer, the galvanometer acts as a voltmeter. The circuit connection is as shown in the figure below.
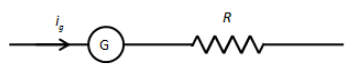
We have given that the galvanometer gives a full scale deflection with 0.006 A current. That means the current through the galvanometer is ig=0.006A.
Let the internal resistance of the galvanometer is r. Now, the potential difference in the above circuit diagram is,
V=igr+igR
⇒V=ig(r+R)
Since the galvanometer is showing the full scale deflection, the maximum voltage across the above circuit is 30 V. Substituting 30 V for V, 0.006 A for ig and 4990Ω for R in the above equation, we get,
30=(0.006)(r+4990)
⇒5000=r+4990
⇒r=5000−4990
⇒r=10Ω
Now, we know that the galvanometer can be converted into an ammeter by connecting a shunt resistance across the galvanometer as shown in the figure below.
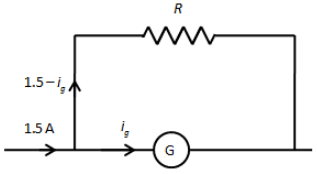
We have given that the range of the ammeter is 1.5 A. Therefore, the total current in the above circuit is 1.5 A, the current in the galvanometer is the same that is ig and the current through the shunt resistance R is 1.5−ig.
We know that the potential drop across the parallel combination remains the same. Therefore, the potential drop at the upper arm and the lower arm is the same.
R(1.5−ig)=igr
We have given the value of shunt resistance, R=2492nΩ.
Substituting R=2492nΩ, ig=0.006A and r=10Ω in the above equation, we get,
(2492n)(1.5−0.006)=(0.006)(10)
⇒2492n=0.040
⇒n=2(0.040)(249)
⇒n=4.98
∴n≈5
Thus, the value of n is 5.
Note: In the question, when the galvanometer is converted into the ammeter, the current flow through the circuit is 1.5 A and this is not the current flow through only the galvanometer. If we put the value of n, the value of shunt resistance becomes 0.040 ohm. Thus, the value of shunt resistance must be very small in order to convert the galvanometer into the ammeter.
