Question

A galvanometer coil has a resistance of $15\Omega$ and the metre shows full scale deflection for a current of $4mA$. How will you convert the metre into an ammeter of range $0A$ to $6A$ ?

Answer 1

Use the formula for the shunt resistance that is to be connected in parallel with the galvanometer. This formula gives the relation between the current for which the galvanometer shows full scale deflection, resistance of the galvanometer and maximum range of the current measured by the ammeter.

Complete step by step answer:
The diagram which represents the conversion of a galvanometer to an ammeter is:

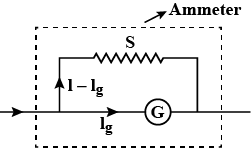
The value of the resistance $S$ of the shunt resistor that should be connected in the circuit to convert the galvanometer into ammeter is given by,
$S = \dfrac{{{I_g}G}}{{I - {I_g}}}........(1)$
Here, ${I_g}$is the current for which the galvanometer shows full scale deflection, $G$is the resistance of the galvanometer and $I$ is the maximum current upto which the range of ammeter (converted from galvanometer) is increased.
We have given that the resistance of the galvanometer coil is $15\Omega$
$G = 15\Omega$
The galvanometer shows the full scale deflection for the current $4mA$
${I_g} = 4mA$
We also have given that the maximum range of the current measured by the ammeter is $6A$
$I = 6A$
Convert the unit of the galvanometer current in the SI system of units.
${I_g} = (4mA)\left( {\dfrac{{{{10}^{ - 3}}A}}{{1mA}}} \right)$
${I_g} = 4 \times {10^{ - 3}}A$
Hence, the current for which the galvanometer shows the full scale deflection is ${I_g} = 4 \times {10^{ - 3}}A$
To convert the galvanometer into an ammeter of the desired range, a shunt resistor of resistance $S$ needs to be converted in parallel with the galvanometer.
We can calculate the value of this shunt resistance using equation (1).
Substitute $4 \times {10^{ - 3}}\Omega$ for ${I_g}$ , $15\Omega$ for $G$ and $6A$ for $I$ in equation (1)
$S = \dfrac{{(4 \times {{10}^{ - 3}}A)(15\Omega )}}{{(6A) - (4 \times {{10}^{ - 3}}A)}}$
$S = \dfrac{{60 \times {{10}^{ - 3}}A}}{{5.996}}$
$S = 10 \times {10^{ - 3}}\Omega$
Now, this can be written as $S = 10m\Omega$
Hence, the shunt resistor of resistance $10m\Omega$ should be connected in parallel to the galvanometer to convert it into a galvanometer of the desired range.

Note: The students should not forget to convert the unit of the current for which the galvanometer shows full scale deflection in the SI system of units because all the physical quantities used in the formula for shunt resistance are in the SI system of units. If this conversion is not done then we will obtain a very large value of the shunt resistance which will be incorrect.