Question

A galvanometer and an unknown resistance in series, is connected across two identical batteries having emf $1.5V$ each. When the batteries are connected in series, the galvanometer records a current of $1A$, and when the batteries are connected in parallel, the current is $0.6A$, then the internal resistance is $\dfrac{1}{{{X}^{1}}}\Omega$. What is the value of ${{X}^{1}}$?

Answer 1

As per the question, first it is connected in series. Find out the net current passing through the circuit. From this derive the equation of net resistance. Now find out the net resistance in the same way when it is connected in parallel. Compare both of them and find out the answer. In this question, don’t forget to consider the internal resistances offered by the batteries.

Complete step by step answer:
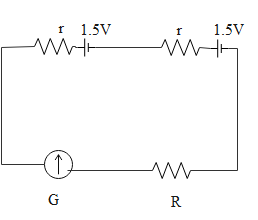
Let us consider $R$ to be the combined resistance of the galvanometer and an unknown resistance in series and $r$ be the internal resistance of each battery. When the batteries, each of emf $E$ are connected in series,
Therefore the net $emf=2E$ and net internal resistance $=2r$.
Therefore the current is given by the formula,
${{i}_{1}}=\dfrac{2E}{R+2r}$
Substituting the values in it,
$1.0=\dfrac{2\times 1.5}{R+2r}$
Hence the net resistance will be equal to,
$R+2r=3$--(1)
Now if the batteries are connected parallel,
The emf remains $E$ and internal resistance becomes $\dfrac{r}{2}$ .
Therefore the current will be
${{i}_{2}}=\dfrac{E}{R+\dfrac{r}{2}}=\dfrac{2E}{2R+r}$
Rearranging the terms will give the equation for net resistance,
$2R+r=\dfrac{2E}{{{i}_{2}}}$
Substituting the values in it,
$2R+r=\dfrac{2\times 1.5}{0.6}=5.0$--(2)
Comparing both the equations internal resistance will give,
$r=\dfrac{1}{3}\Omega$
Therefore we can write that,
${X}'=3\Omega$

So, the correct answer is “$r=\dfrac{1}{3}\Omega$”.

Note: Internal resistance is given as the resistance offered to the flow of current by the cells and batteries themselves which will result in the generation of heat. Internal resistance is also calculated in Ohms. Heating the battery will spontaneously lower the internal resistance and works extra runtime.