Question

A Galilean telescope measures 9 cm from the objective to the eye-piece. The focal length of the objective is 15 cm. Its magnifying power is
A. $2.5$
B. $\dfrac{2}{5}$
C. $\dfrac{5}{3}$
D. $\dfrac{3}{5}$

Answer 1

In a Galilean telescope, the focal length of the objective lens is equal to the difference between the length between the two lenses and the focal length of the eye-piece, ${f_o} = L + {f_e}$, where ${f_o},{f_e}$ are the focal lengths of objective lens and eye-piece, L is the distance between them. Substitute the values of L and focal length of the objective lens to find the value of focal length of the eye-piece. Magnification is the negative ratio of focal length of the objective lens and focal length of the eye-piece.

Complete step by step answer:

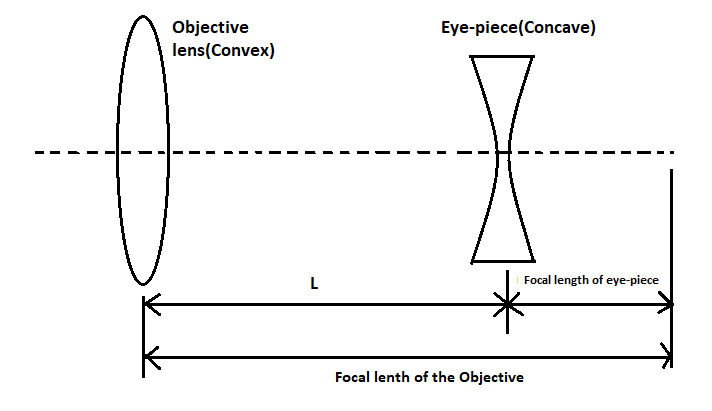We are given that a Galilean telescope measures 9 cm from the objective to the eye-piece and the focal length of the objective is 15 cm.
We have to find its magnifying power.
As we can see in the above figure, the objective is a convex lens and the eye-piece is a concave lens.
So the focal length is negative for the concave (eye-piece) lens.
As we can see, the focal length of the objective lens is the sum of the focal length of the eye-piece and the distance between them.
${f_o} = L + {f_e}$, where ${f_o},{f_e}$ are the focal lengths of objective lens and eye-piece, L is the distance between them and ${f_e}$ should be taken negatively.
${f_o} = L + \left( { - {f_e}} \right) \\\ \implies {f_o} = L - {f_e} \\\ \implies {f_e} = L - {f_o} \\\$
Substitute the values of the L and ${f_o}$ as they are given in the question.
${f_o} = 15cm,L = 9cm \\\ \implies {f_e} = L - {f_o} \\\ = 9 - 15 \\\ \therefore {f_e} = - 6cm \\\$
Magnification is the negative ratio of focal length of the objective lens and focal length of the eye-piece.
$m = \dfrac{{ - {f_o}}}{{{f_e}}} \\\ {f_o} = 15cm,{f_e} = - 6cm \\\ m = \dfrac{{ - 15}}{{ - 6}} \\\ \implies m = \dfrac{5}{2} \\\ \therefore m = + 2.5 \\\$
The magnifying power of the given Galilean telescope is 2.5.
So, the correct answer is “Option A”.

Note:
The objective lens is concave, which is a spherical lens and focuses the light rays passed through it to a specific point. Eye-piece is a convex lens, which is a spherical lens and diverges the light rays refracted from it. The lenses used in objective and eye-piece are not the same in a Galilean telescope. Be careful in considering the lenses.