Question

A function f: R→R has property $f(x + y) = f(x)·e^{f(y)-1}$, for every x, y ∈ R then positive value of f (4)

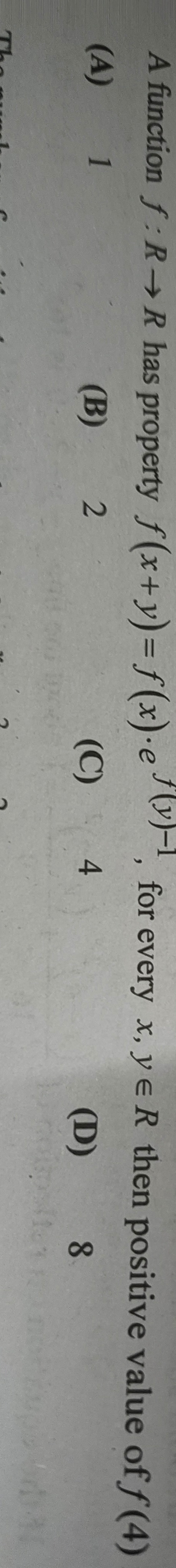
• A. 1
• B. 2
• C. 4
• D. 8

Answer 1

Answer: (A)

1

Answer 2

We are given $f(x+y) = f(x) \cdot e^{f(y)-1} \quad \forall x,y\in\mathbb{R}.$

1. Find $f(0)$:

Set $y=0$: $f(x+0)=f(x) \cdot e^{f(0)-1}\quad\Rightarrow\quad f(x) = f(x) \cdot e^{f(0)-1}.$

For nonzero $f(x)$, $e^{f(0)-1} = 1 \quad\Rightarrow\quad f(0)-1=0 \quad\Rightarrow\quad f(0)=1.$

2. Obtain an equation for $f(y)$:

Set $x=0$: $f(y)=f(0) \cdot e^{f(y)-1}=e^{f(y)-1}.$

Let $u = f(y)$. Thus, $u = e^{u-1}.$

Taking the natural logarithm (when $u>0$) we have $\ln u = u-1.$

It is easy to verify that $u=1$ is a solution because $\ln 1 = 0 \quad \text{and} \quad 1-1 = 0.$

Since this holds for every $y$, we conclude that $f(y)=1 \quad \forall y\in\mathbb{R}.$

Therefore, $f(4)=1.$