Question

A fruit grower can use two types of fertilizer in his garden, brand P and brand Q. The amounts (in kg) of nitrogen, phosphoric acid, potash, and chlorine in a bag of each brand are given in the table. Tests indicate that the garden needs at least 240 kg of phosphoric acid, at least 270 kg of potash and at most 310 kg of chlorine.
If the grower wants to minimize the amount of nitrogen added to the garden, how many bags of each brand should be used? What is the minimum amount of nitrogen added in the garden?

Kg per bag	Brand P	Brand Q
Nitrogen	3	3.5
Phosphoric acid	1	2
Potash	3	1.5
Chlorine	1.5	2

Answer 1

Here we will first find the constraint equations from the data given in the question. Then we will find the objective function for the minimum amount of nitrogen. We will plot the constraints in the graph and then find the corner points. We will then check at which corner point the objective function is minimum.

Complete step-by-step answer:
First, we will assume the number of packages of brand P required and the package of brand Q required. Therefore
Let $X$ be the number of packages of brand P required and $Y$ be the number of packages of brand Q required.
Now we will make the conditional statements from the data given in the question.
It is given that the garden needs at least 240 kg of phosphoric acid. Since the bag of brand P contains 1 kg and the bag of brand Q contains 2 kg of Phosphoric acid. So, from this we will form an equation, we get
$X + 2Y \ge 240$…………………….$\left( 1 \right)$
It is given that the garden needs at least 270 kg of potash. Since the bag of brand P contains 3 kg and the bag of brand Q contains 1.5 kg of potash. So, from this we will form an equation, we get
$3X + 1.5Y \ge 270$
Dividing both sides by $1.5$, we get
$\Rightarrow$ $2X + Y \ge 180$…………………….$\left( 2 \right)$
It is given that the garden needs at most 310 kg of chlorine. Since the bag of brand P contains 1.5 kg and the bag of brand Q contains 2 kg of chlorine. So, from this we will form an equation, we get
$1.5X + 2Y \le 310$…………………….$\left( 3 \right)$
Also we know that the quantity of the packages required cannot be negative. Therefore, we get
$X \ge 0$ and $Y \ge 0$…………………….$\left( 4 \right)$
Now we have to make the objective function of the equation. As we have the minimum amount of nitrogen added in the garden. It is given that the Bag of brand P contains 3 kg of Nitrogen and Bag of brand Q contains $3.5$ kg of Nitrogen.
Therefore, the objective function is $Z = 3X + 3.5Y$.
Now we have to plot all the equations constraints from the equations $\left( 1 \right)$, $\left( 2 \right)$, $\left( 3 \right)$ and $\left( 4 \right)$ in the graph to get the feasible region.
Now we will get all the corner points and check at what point the value of minimum amount of nitrogen.

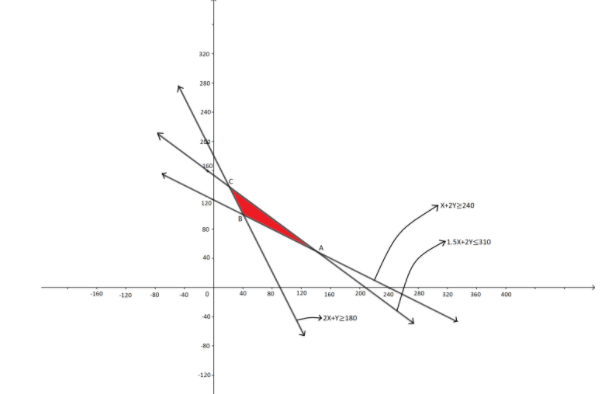
Hence, there are three corner points of the feasible region i.e. $A\left( {140,50} \right),B\left( {40,100} \right),C\left( {20,140} \right)$.
Now, we will find the value of the objective function at every corner point and find that corner point at which the objective function is minimum. Therefore, we get
Objective function at corner point $A\left( {140,50} \right)$ is
$\Rightarrow$ $Z = 3\left( {140} \right) + 3.5\left( {50} \right) = 595$
Objective function at corner point $B\left( {40,100} \right)$ is
$\Rightarrow$ $Z = 3\left( {40} \right) + 3.5\left( {100} \right) = 470$
Objective function at corner point $C\left( {20,140} \right)$ is
$\Rightarrow$ $Z = 3\left( {20} \right) + 3.5\left( {140} \right) = 550$
So, we can clearly see that the objective function is minimum at corner point $B\left( {40,100} \right)$ i.e. at $X = 40$ and $Y = 100$.
Hence, the number of packages of brand P required are 40 and the package of brand Q required are 100 to minimize the amount of nitrogen added in the garden.
Hence, the minimum amount of nitrogen added in the garden is equal to 470kg.

Note: Here we have to note that the constraints equation should be formed carefully. While forming the equations we don’t have to convert the amount given in Kg into any other measuring units. We have to note that we cannot take the origin as the corner point then the value of the objective function will be zero.
Feasible region is the search space or the solution space where the value of the objective function is optimal. Maximum and the minimum value of the objective function are generally at the corner points of the feasible region.