Question
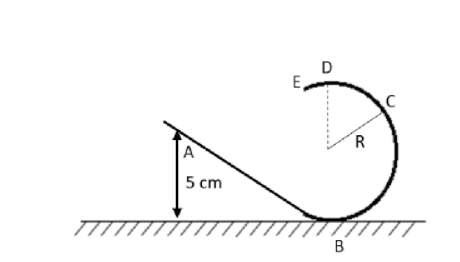
Question: A frictionless track ABCDE ends in a circular loop of radius \[R\]. A body slides down the track fro...
A frictionless track ABCDE ends in a circular loop of radius R. A body slides down the track from point A which is at height h=5cm. Find the maximum value of R for a body to complete the loop successfully.
A. 2cm
B. 310cm
C. 415cm
D. 315cm
Solution
Use the formula for kinetic energy of an object and potential energy of an object. Use the formula for velocity of an object at the bottom of the vertical circle. Apply law of conservation of energy at the points A and B of the track ABCDE and determine the value of radius necessary for the body to complete the circular loop.
Formulae used:
The kinetic energy K of an object is
K=21mv2 …… (1)
Here, m is the mass of the object and v is the velocity of the object.
The potential energy U of an object is
U=mgh …… (2)
Here, m is the mass of the object, g is acceleration due to gravity and h is the height of the object from the ground.
Complete step by step answer:
We have given that a body at point A moves on the track ABCDE. The track forms a circular loop of radius R.
Initially at point A, the height of the body from ground is 5cm.
h=5cm
We are asked to determine the radius R of the circular track so that the body completes the circular loop.
The potential energy of the body at point A is given by
UA=mgh
Substitute 5cm for h in the above equation.
UA=mg(5cm)
⇒UA=5mg
The velocity of the body to complete the circular loop at point B should be
vB=5gR
The kinetic energy of the body at the bottom point B of the circular loop is given by
KB=21mvB2
Substitute 5gR for vB in the above equation.
KB=21m(5gR)2
⇒KB=25mgR
We know that according to the law of conservation of energy, the potential energy of body at point A must be equal to the kinetic energy of the body at point B.
UA=KB
Substitute 5mg for UA and 25mgR for KB in the above equation.
5mg=25mgR
⇒R=2cm
Therefore, the radius of the circular loop should be 2cm.
Hence, the correct option is A.
Note: The students should keep in mind that the kinetic energy of the body is zero when it starts from point A as it starts from rest and the potential energy of the body at point B is zero as the height of the body at point B is zero from the ground. Hence, the potential energy of the body at point A is equal to kinetic energy at point B.
