Question

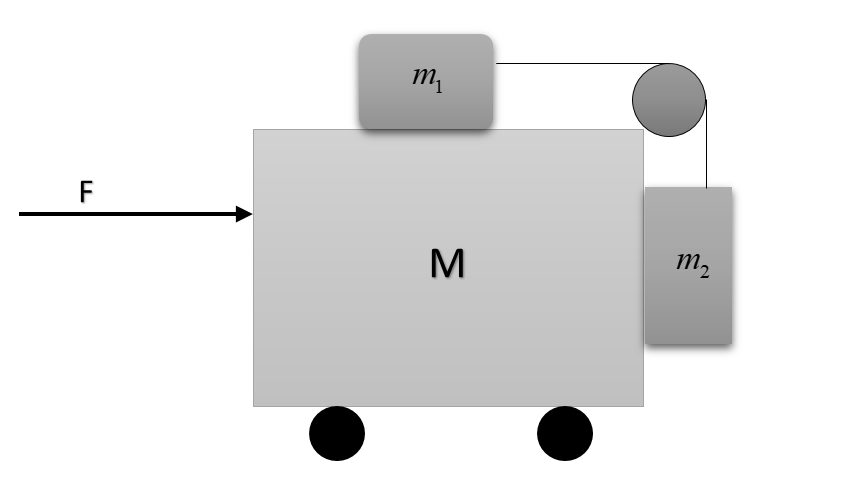
A frictionless cart of mass M carries two other frictionless carts having masses $m_1\ and \ m_2$ connected by a string passing over a pulley as shown in figure. The horizontal force that must be applied on M so that $m_1\ and \ m_2$do not move relative to it will be:
$\text A. \quad (M+m_1+m_2)(m_2/m_1)g$
$\text B. \quad (M+m_1+m_2)(m_1/m_2)g$
$\text C. \quad (M+m_1)(m_2/m_1)g$
$\text D. \quad (M+m_2)(m_2/m_1)g$

Answer 1

The limitation of Newton's laws of motion is that they are valid only for inertial frames of reference. These are not valid for frame moving with some acceleration. Hence, to apply these laws, physicists suggested that we must apply an imaginary force on the system called a pseudo force which will act on the centre of mass of the body and has direction opposite to the motion of the frame.

Formula used: F = ma

Complete step by step answer:
The first and foremost thing is to draw the free body diagram of the system.

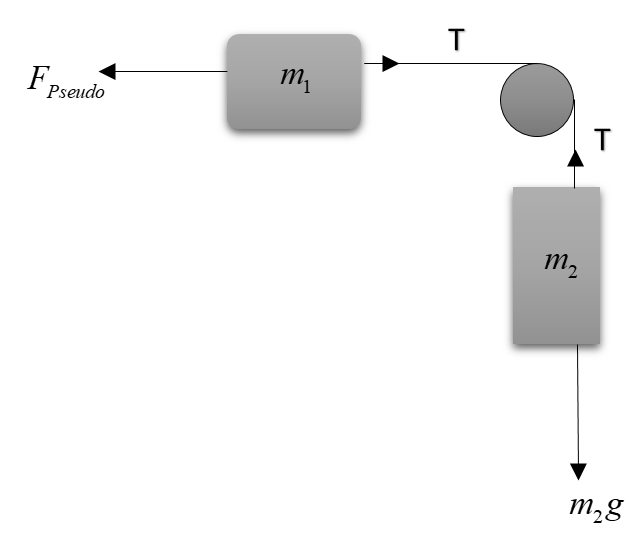
Here, we’ve shown only the important forces that will take us to the final result.
Concept used – We just have to reach that value so that the pseudo force on $m_1$ balances the weight of $m_2$.
Now, using ‘F’, we can write the equation as $F = m_T a$, where $m_T$ is the total mass of the system.
Thus, $F = (M+m_1 +m_2)a$
$\implies a = \dfrac{F}{M+m_1+m_2}$
Now, pseudo force acting of upper block will be:
$F_{Pseudo} = m_1 a = \dfrac{m_1 F}{M+m_1+m_2}$
This should balance the weight of $m_2$, hence:
$m_2 g = \dfrac{m_1 F}{M+m_1+m_2}$
$\implies F = (M+m_1+m_2)(m_2 /m_1) g$
So, the correct answer is “Option A”.

Note: It must be noted that we’ve taken only contributing forces while making free body diagrams as showing all forces will create unnecessary calculations and confusions. On both the blocks, the weight is acting. But we’ve shown only the weight of $m_2$ as only it will contribute to the motion of blocks. Similarly pseudo force is acting on both the blocks, but we’ve shown it only for the upper block. In case friction, we have to take each and every force including normal reactions, contact forces, etc. and then analyze the situation properly.