Question

A block of mass 10 kg is released from the top of smooth wedge (whose inclination at $\theta$ = 37°) which is moving with a constant velocity 10 m/s. The work done by the force applied by wedge on the block in 2 sec will be (in joules) :-

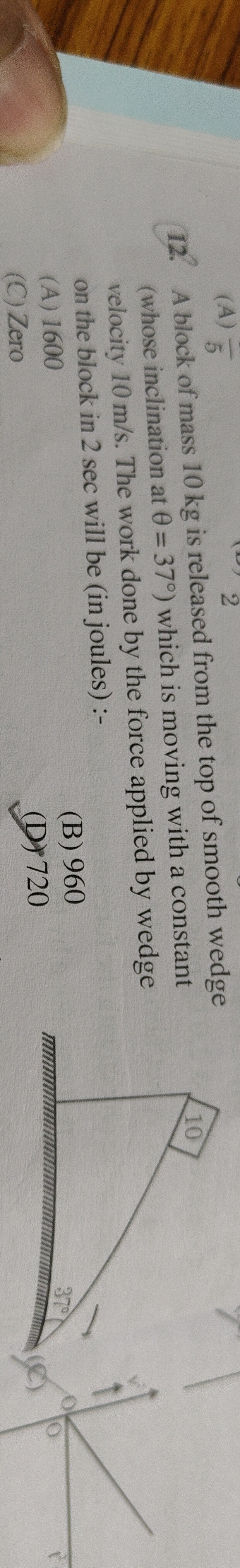
• A. 1600
• B. 960
• C. Zero
• D. 720

Answer 1

Answer: (B)

960

Answer 2

To solve this problem, we need to calculate the work done by the normal force applied by the wedge on the block. The work done by a force is given by $W = \vec{F} \cdot \vec{d}$, where $\vec{F}$ is the force and $\vec{d}$ is the displacement of the point of application of the force.

1. Identify the force: The force applied by the wedge on the block is the normal force, $\vec{N}$.

2. Determine the normal force magnitude: The block is on a smooth wedge, so there is no friction. The forces acting on the block are gravity ($mg$) and the normal force ($N$). The component of gravity perpendicular to the incline is $mg \cos\theta$. Since there is no acceleration perpendicular to the incline, the normal force balances this component: $N = mg \cos\theta$ Given: $m = 10$ kg, $\theta = 37^\circ$. We use $g = 10 \text{ m/s}^2$ (a common approximation in such problems unless specified otherwise). We know $\cos 37^\circ \approx 4/5 = 0.8$. $N = (10 \text{ kg})(10 \text{ m/s}^2)(4/5) = 100 \times (4/5) = 80$ N.

3. Determine the normal force vector: From the diagram, the wedge's inclined surface rises from left to right. If the block is on top of this wedge, the normal force $\vec{N}$ acts perpendicular to the surface, pointing upwards and to the left. The angle the incline makes with the horizontal is $\theta = 37^\circ$. The normal force vector $\vec{N}$ makes an angle of $(90^\circ + \theta)$ with the positive x-axis (horizontal right). So, $\vec{N} = N (\cos(90^\circ + \theta) \hat{i} + \sin(90^\circ + \theta) \hat{j})$ $\vec{N} = N (-\sin\theta \hat{i} + \cos\theta \hat{j})$ Using $\sin 37^\circ \approx 3/5 = 0.6$ and $\cos 37^\circ \approx 4/5 = 0.8$: $\vec{N} = 80 \text{ N} (-0.6 \hat{i} + 0.8 \hat{j}) = (-48 \hat{i} + 64 \hat{j})$ N.

4. Determine the displacement of the point of application of the force: The work done by the normal force is $W_N = \int \vec{N} \cdot d\vec{r}_{block}$. The displacement of the block relative to the ground ($\vec{r}_{block}$) can be expressed as the sum of the displacement of the wedge ($\vec{r}_{wedge}$) and the displacement of the block relative to the wedge ($\vec{r}_{block/wedge}$): $\vec{r}_{block} = \vec{r}_{wedge} + \vec{r}_{block/wedge}$. So, $W_N = \int \vec{N} \cdot (d\vec{r}_{wedge} + d\vec{r}_{block/wedge})$. Since the normal force $\vec{N}$ is always perpendicular to the surface of the wedge, and the displacement of the block relative to the wedge ($d\vec{r}_{block/wedge}$) is always along the surface of the wedge, the dot product $\vec{N} \cdot d\vec{r}_{block/wedge} = 0$. Therefore, the work done by the normal force simplifies to: $W_N = \int \vec{N} \cdot d\vec{r}_{wedge} = \vec{N} \cdot \vec{d}_{wedge}$ (since $\vec{N}$ is constant).

5. Determine the displacement of the wedge: The wedge is moving with a constant velocity of 10 m/s for 2 seconds. The problem does not specify the direction of the wedge's velocity. Let's consider two possibilities for the direction of the wedge's velocity:

   • Case 1: Wedge moves to the right. $\vec{v}_{wedge} = 10 \hat{i}$ m/s. $\vec{d}_{wedge} = \vec{v}_{wedge} t = (10 \hat{i} \text{ m/s})(2 \text{ s}) = 20 \hat{i}$ m. $W_N = \vec{N} \cdot \vec{d}_{wedge} = (-48 \hat{i} + 64 \hat{j}) \cdot (20 \hat{i})$ $W_N = (-48)(20) + (64)(0) = -960$ J.
   • Case 2: Wedge moves to the left. $\vec{v}_{wedge} = -10 \hat{i}$ m/s. $\vec{d}_{wedge} = \vec{v}_{wedge} t = (-10 \hat{i} \text{ m/s})(2 \text{ s}) = -20 \hat{i}$ m. $W_N = \vec{N} \cdot \vec{d}_{wedge} = (-48 \hat{i} + 64 \hat{j}) \cdot (-20 \hat{i})$ $W_N = (-48)(-20) + (64)(0) = 960$ J.

6. Conclusion: Since the options provided are all positive values, and 960 J is one of the options (B), it is highly probable that either the problem implies the wedge is moving to the left, or it asks for the magnitude of the work done. In the context of multiple-choice questions where only positive options are given for a quantity that can be negative, the magnitude is often implied.

The work done by the force applied by the wedge on the block is 960 Joules.