Question
Question: Principal solutions of the equation $sin2x + cos2x = 0$, where $\pi < x < 2\pi$ are,...
Principal solutions of the equation sin2x+cos2x=0, where π<x<2π are,
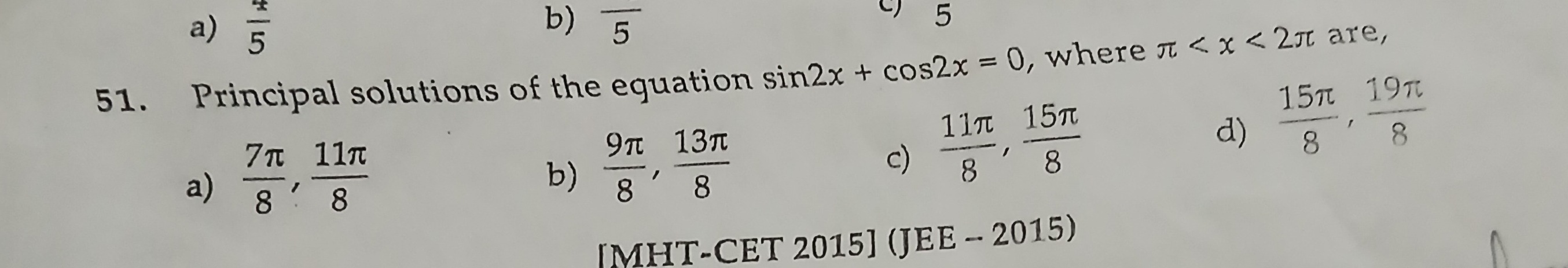
A
87π,811π
B
89π,813π
C
811π,815π
D
815π,819π
Answer
811π,815π
Explanation
Solution
We start with the equation:
sin2x+cos2x=0This can be rearranged as:
sin2x=−cos2x⟹tan2x=−1(cos2x=0)Thus, the general solution for 2x is:
2x=−4π+kπ,k∈ZTherefore,
x=−8π+2kπNow, we need to determine values of k such that:
π<x<2πFor k=3:
x=−8π+23π=−8π+812π=811πFor k=4:
x=−8π+24π=−8π+816π=815πThese values lie in the required interval.
