Solveeit Logo
Login

Question

Question: The value of $\sin^{-1}(\frac{12}{13})-\sin^{-1}(\frac{3}{5})$ is equal to...

The value of sin⁡−1(1213)−sin⁡−1(35)\sin^{-1}(\frac{12}{13})-\sin^{-1}(\frac{3}{5}) is equal to

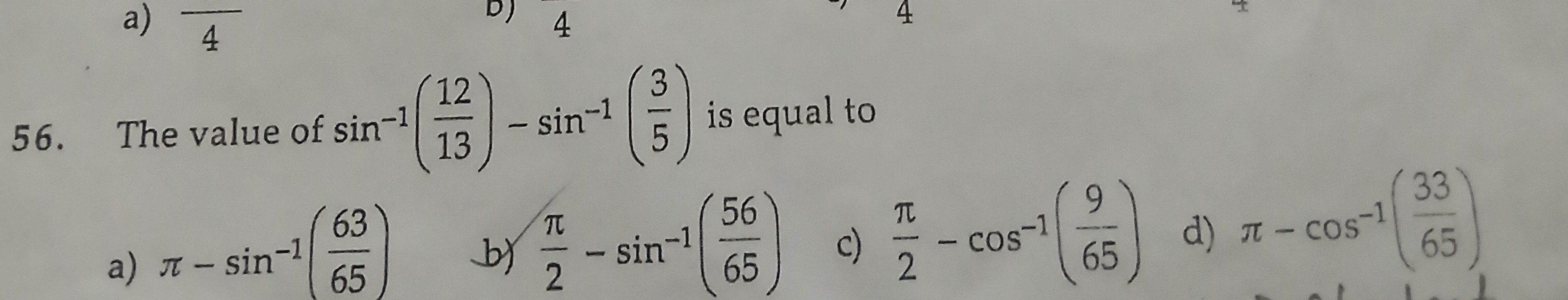
A

π−sin⁡−1(6365)\pi-\sin^{-1}(\frac{63}{65})

B

π2−sin⁡−1(5665)\frac{\pi}{2}-\sin^{-1}(\frac{56}{65})

C

π2−cos⁡−1(965)\frac{\pi}{2}-\cos^{-1}(\frac{9}{65})

D

π−cos⁡−1(3365)\pi-\cos^{-1}(\frac{33}{65})

Answer

Option b) π2−sin⁡−1(5665)\frac{\pi}{2}-\sin^{-1}\left(\frac{56}{65}\right)

Explanation

Solution

Let

A=sin⁡−1(1213)andB=sin⁡−1(35).A = \sin^{-1}\left(\frac{12}{13}\right) \quad \text{and} \quad B = \sin^{-1}\left(\frac{3}{5}\right).

Then

sin⁡A=1213,cos⁡A=1−(1213)2=513,\sin A=\frac{12}{13},\quad \cos A=\sqrt{1-\left(\frac{12}{13}\right)^2}=\frac{5}{13}, sin⁡B=35,cos⁡B=1−(35)2=45.\sin B=\frac{3}{5},\quad \cos B=\sqrt{1-\left(\frac{3}{5}\right)^2}=\frac{4}{5}.

Using the sine difference formula:

sin⁡(A−B)=sin⁡Acos⁡B−cos⁡Asin⁡B=1213⋅45−513⋅35=4865−1565=3365.\sin(A-B)=\sin A\cos B-\cos A\sin B=\frac{12}{13}\cdot\frac{4}{5}-\frac{5}{13}\cdot\frac{3}{5}=\frac{48}{65}-\frac{15}{65}=\frac{33}{65}.

Since A−BA-B is in the principal range [−π2,π2][-\frac{\pi}{2},\frac{\pi}{2}], we have:

A−B=sin⁡−1(3365).A-B = \sin^{-1}\left(\frac{33}{65}\right).

Notice that

sin⁡−1(3365)=π2−cos⁡−1(3365).\sin^{-1}\left(\frac{33}{65}\right) = \frac{\pi}{2} - \cos^{-1}\left(\frac{33}{65}\right).

Also, since cos⁡−1(3365)=sin⁡−1(1−(3365)2)\cos^{-1}\left(\frac{33}{65}\right)=\sin^{-1}\left(\sqrt{1-\left(\frac{33}{65}\right)^2}\right) and

1−(3365)2=1−10894225=31364225=5665,\sqrt{1-\left(\frac{33}{65}\right)^2}=\sqrt{1-\frac{1089}{4225}}=\sqrt{\frac{3136}{4225}}=\frac{56}{65},

it follows that

cos⁡−1(3365)=sin⁡−1(5665).\cos^{-1}\left(\frac{33}{65}\right)=\sin^{-1}\left(\frac{56}{65}\right).

Therefore,

A−B=π2−sin⁡−1(5665).A-B = \frac{\pi}{2} - \sin^{-1}\left(\frac{56}{65}\right).

Thus, the correct option is:

Option b) π2−sin⁡−1(5665)\frac{\pi}{2}-\sin^{-1}\left(\frac{56}{65}\right).