Solveeit Logo
Login

Question

Question: A force \( {\text{F}} = {\text{i}} + 4{\text{j}} \) acts on the block shown. The force of friction a...

A force F=i+4j{\text{F}} = {\text{i}} + 4{\text{j}} acts on the block shown. The force of friction acting on the block is:
(A) −i- i
(B) −18i- 18i
(C) −2.4i- 2.4i
(D) −3i- 3i

Explanation

Solution

A vector of force is a representation of a force which has both magnitude and direction. This is opposed to simply giving the force magnitude, which is referred to as a scalar quantity. A vector is typically represented in the direction of the force by an arrow and with a length proportional to the magnitude of the force.

Formula used:
We will use the following formula to solve this question:
fs=μN{f_s} = \mu N
Where
fs{f_s} is the maximum frictional force that can happen of a force FF is applied
μ\mu is the coefficient of friction
NN is the normal force

Complete step by step answer:

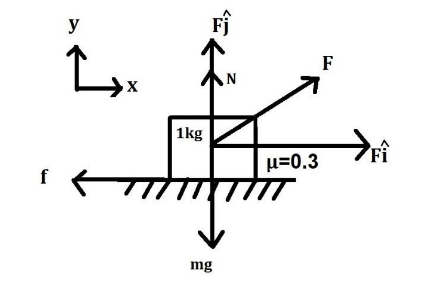
According to the question, the mass of the body is 1kg1kg
Let us suppose g=10m/s2g = 10m/{s^2}
Then the weight of the system will be mg=1×10=10Nmg = 1 \times 10 = 10N
We can breakdown all the forces acting on the body as per the figure above
Force in the X-axis is Fi^=1Ni^F\hat i = 1N\hat i
Force in the Y-axis is Fj^=4Nj^F\hat j = 4N\hat j
We can see that along Y-axis, the system is in equilibrium
Now we will balance all the forces action along the Y-axis
So, we get
Fj^+N=mgF\hat j + N = mg
⇒N=mg−Fj^\Rightarrow N = mg - F\hat j
Now we will put the values in the equation above to get,
∴N=10−4=6N\therefore N = 10 - 4 = 6N
Then the maximum frictional force that can be applied if a force FF is applied,
fs=μ×N{f_s} = \mu \times N
⇒fs=0.3×6\Rightarrow {f_s} = 0.3 \times 6
So, we get
∴fs=1.8N\therefore {f_s} = 1.8N
Also, force in X-axis is 1N1N
And the maximum frictional force that can be applied is 1.8N1.8N
Therefore, the force is not enough to overcome the frictional force
So, the frictional force will be equal but opposite to the applied force
Hence, fs=−i{f_s} = - i Correct option is (A.)

Note:
A major feature of force vectors is that, according to the application of the force, they can be broken into components. Vector components are generally perpendicular to each other, although a parallelogram configuration can also be used.