Question

A force $\overrightarrow{{{F}_{1}}}=A\widehat{j}$ is applied to a point whose radius vector is $\overrightarrow{{{r}_{1}}}=a\widehat{i}$, while a force $\overrightarrow{{{F}_{2}}}=B\widehat{i}$ is applied to the point whose radius vector $\overrightarrow{{{r}_{2}}}=b\widehat{j}$. Both radius vectors are determined relative to the origin of coordinates$O$. It is given that $\widehat{i}$ and $\widehat{j}$ are the unit vectors of the x and y axes and $a,b,A,B$ are constants. Find the arm $l$ of the resultant force relative to the point $O$.

$\text{A}\text{. }l\text{=}\dfrac{aA-bB}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$
$\text{B}\text{. }l=\dfrac{aA+bB}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$
$\text{C}\text{. }l=\dfrac{aA-bB}{\sqrt{{{A}^{2}}-{{B}^{2}}}}$
$\text{D}\text{. None of these}$

Answer 1

Hint: We will find the resultant of the vectors $\overrightarrow{{{F}_{1}}}=A\widehat{j}$ and $\overrightarrow{{{F}_{2}}}=B\widehat{i}$ using vector addition method. The normal force vector will be perpendicular to both the vectors. Magnitude of the arm can be obtained by dividing the Normal vector and the Resultant vector.

Complete step by step answer:
A force vector is the representation of a force that has both magnitude and direction. Force vectors can be broken into components according to the application of the force. A radius vector is a line of variable length from a fixed origin to a curve. We can also say that a radius vector is the length of the line segment joining a fixed point or origin to a given point. The normal vector to a surface is the vector which is perpendicular to the surface at a given point.

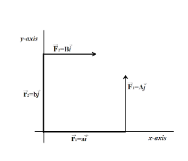
A resultant vector is the combination of two or more single vectors. It is the result obtained by adding two or more vectors together. The resultant force vector can be determined by adding the individual forces together using vector addition method.

We are given two vectors $\overrightarrow{{{F}_{1}}}=A\widehat{j}$and $\overrightarrow{{{F}_{2}}}=B\widehat{i}$having radius vectors $\overrightarrow{{{r}_{1}}}=a\widehat{i}$and $\overrightarrow{{{r}_{2}}}=b\widehat{j}$respectively.

$\begin{aligned}

&\overrightarrow{N}=\overrightarrow{{{r}{1}}}\times \overrightarrow{{{F}{1}}}+\overrightarrow{{{r}{2}}}\times \overrightarrow{{{F}{2}}}=\left( a\widehat{i}\times A\overrightarrow{j} \right) \\
& =ab\overrightarrow{k}+AB\left( -\overrightarrow{k} \right) \\
& =(ab-AB)\overrightarrow{k}
\end{aligned}$

Resultant of the external force,

$\overrightarrow{F}=\overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}}=A\overrightarrow{j}+B\overrightarrow{j}$
As $\overrightarrow{N}\bot \overrightarrow{F}$
Therefore, $\overrightarrow{N}\cdot \overrightarrow{F}=0$
Now, $l=\dfrac{N}{F}$
$l=\dfrac{ab-AB}{\sqrt{{{A}^{2}}+{{B}^{2}}}}$
Hence, the correct option is A.

Note:
While working with vectors, students must be very careful in choosing the right direction of the vector in the Cartesian plane. In the above question, representation of force vectors and the radius vectors should be done as per the given unit vectors along the direction of the force vectors.