Question

A force of 98 newtons is required to just drag a body of mass 100 kg on ice. The coefficient of friction will be
A. 0.98
B. 0.89
C. 0.49
D. 0.10

Answer 1

The friction basically means, a resistance or obstruction offered to the application of a force against another surface.
Mathematically, the frictional force is directly proportional to the normal reaction provided by the surface for the body.
Frictional force
$F_s \propto N$
By removing the sign of proportionality and introducing a constant, we have:
$F_s = \mu N$
Where $\mu$ is called the coefficient of friction.

Complete step by step answer:
Let us consider the body of mass 100 kg on ice

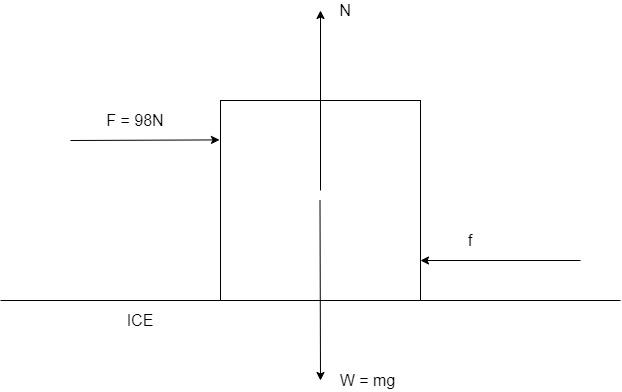
Here, there are 4 forces acting on the block. They are
i) Weight of the body, $W = mg$
ii) Normal force acted by the surface, $N$
iii) Force applied to move, $F = 98N$
iv) Frictional force, $f = \mu N$
Since the body just starts to move, the force applied to move the body is equal to the frictional force acting on it by the surface.
We see that the body is in equilibrium with all the forces acting on it. Hence,
Vertical forces: $W = N$
Horizontal forces: $F = f$
Given, mass m = 100 kg.
Weight, $W = mg = 100 \times 9.8 = 980N$ (assuming the acceleration due to gravity, $g = 9.8m{s^{ - 2}}$)
This weight is equal to the normal:
$W = N = 980N$
Also, we have
$F = f = \mu N$
Given, $F = 98 N$.
Substituting the values of F and N, we have
$\Rightarrow F = \mu N$
$\Rightarrow 98 = \mu \times 980$
$\Rightarrow \mu = \dfrac{{98}}{{980}} = \dfrac{1}{{10}} = 0.1$

Therefore, the coefficient of friction is, $\mu = 0.1$. Hence, the correct option is Option D.

Note:
The students should note that the force applied here, is equal to the kind of friction called impending friction. Impending friction is the friction applied to the body when the body is just about to start moving. Any applied force that is lesser than this particular value of impending friction, is termed as static friction.