Question

A force of $72\,dyne$ is inclined to the horizontal at an angle of $60^\circ$ .Find the acceleration it produces in a mass of $9g$ which moves in a horizontal direction.

Answer 1

With the help of the problem statement, first, draw a rough diagram, then split force into its two components as the body accelerates in the direction of the horizontal component, equate the horizontal component with the force produced due to acceleration of the body which is the product of mass with the acceleration. Now we can find the acceleration by solving.

Complete step by step answer:
Force: A force is a push or pull upon an object with the object having some mass that causes it to change its velocity and this change in velocity is known as acceleration.
$F = ma$
Where, Force = $F$, Mass of the object = $m$ and Acceleration due to change in velocity = $a$.

As per the problem, a force of $72\,dyne$ is inclined to the horizontal at an angle of $60^\circ$. To need to calculate the acceleration of the body, mass of $9g$ which moves in a horizontal direction. We know,
$F = 72\,dyne$
$\Rightarrow \theta = 60^\circ$
$\Rightarrow m = 9g$

Now with the help of all this information, we can draw a rough diagram:

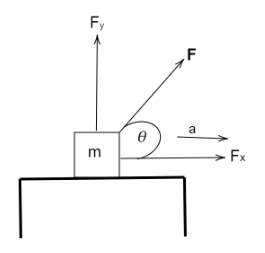
From the diagram, the force applied on the body is inclined at an angle of $60^\circ$ with the horizon.Hence the component of the force along,
Horizontal Direction:
$F_x = F\cos \theta$
Vertical Direction:
$F_y = F\sin \theta$
The body of mass $9g$ accelerates in the horizontal direction.
Now we can write,
$F_x = ma_x$
Where $F_x = F\cos \theta$

Putting this value in the above formula qwe will get,
$F\cos \theta = ma_x$
By putting all the know value in the above formula we will get,
$72\,dyne \times \cos 60^\circ = 9g \times a_x$
Where,
$1\,dyne = 1g\,cm\,{s^{ - 2}}$
$\Rightarrow 72\,dyne = 72g\,cm\,{s^{ - 2}}$
Replacing this dyne value in the above equation we will get,
$72\,g\,cm\,{s^{ - 2}} \times \cos 60^\circ = 9g \times a_x$
We know, $\cos 60^\circ = \dfrac{1}{2}$

Putting this value in the above equation we will get,
‘$72\,g\,cm\,{s^{ - 2}} \times \dfrac{1}{2} = 9g \times a_x$
$\Rightarrow 36\,g\,cm\,{s^{ - 2}} = 9g \times a_x$
Rearranging the above equation we will get,
$\dfrac{{36\,g\,cm\,{s^{ - 2}}}}{{9g}} = a_x$
Dividing both numerator and denominator by $9g$ in LHS we will get,
$4\,cm\,{s^{ - 2}} = a_x$
$\therefore a_x = 4\,cm\,{s^{ - 2}}$

Hence it produces an acceleration of $4\,cm\,{s^{ - 2}}$ in the body of mass $9g$ which moves in a horizontal direction.

Note: Remember no need to calculate the vertical force acting on the block as there is no motion along the vertical direction hence the force due to gravity and the vertical force on the block cancel out each other. Another important thing to remember is that $1\,N = {10^5}\,dyne$.