Question

A force of 60N acting perpendicular to a force of 80N can produce
A. 20N
B. 70N
C. 100N
D. 140N

Answer 1

As we know that the force is a vector quantity that is, it has both magnitude and direction. Thus to add two forces we need to add them vectorially. As the given two forces are perpendicular to each other thus we can use Pythagoras Theorem to calculate the resultant of the given two forces.

Complete step-by-step solution :
When scalar quantities are used to perform calculations, then normal rules of arithmetic are applied; but when vector quantities are involved, the process is more composite since the direction of the vector must be taken into account.
A vector quantity can be represented graphically by a straight line with an arrow-head at its end. The direction in which the arrow points gives the sense of the vector and the length of the line indicates the vector's magnitude.
When two or more vectors are used to describe a process, these vectors can be replaced by a single resultant vector that carries the equivalent information of original vectors.
And we are asked to calculate the same resultant vector of the forces
${\vec F_1} = 60N$ , ${\vec F_2} = 80N$
Given force vectors can be arranged as below:

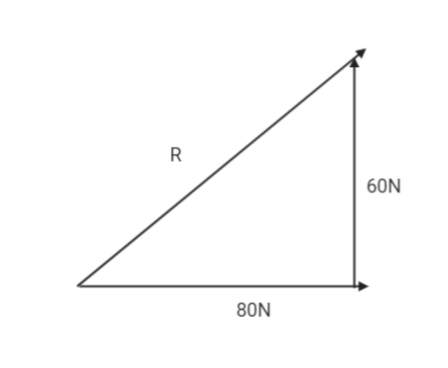
Now using Pythagoras theorem we can easily calculate the resultant force.
${\vec F_R} = {\vec F_1} + {\vec F_2}$
${\vec F_R} = \sqrt {{{60}^{}} + {{80}^2}}$
${\vec F_R} = \sqrt {3600 + 6400}$
${\vec F_R} = \sqrt {10000} = 100N$
Hence, option C is correct.

Note:- To add many vectors we can even use direction system ( $\hat i,\hat j,\hat k$ ) to calculate the resultant of these forces with the direction.
Suppose the given vector is $F = x\hat i + y\hat j + z\hat k$
Then its magnitude can be calculated as $|F| = \sqrt {{x^2} + {y^2} + {z^2}}$