Question
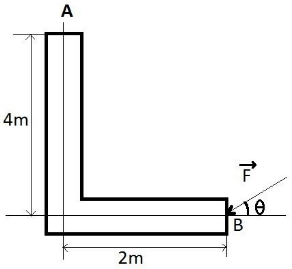
Question: A force of \(40N\) acts on a point B at the end of an L-shaped object, as shown in figure. The angle...
A force of 40N acts on a point B at the end of an L-shaped object, as shown in figure. The angle θ that will produce maximum moment of the force about point A is given by:
A. tanθ=41
B. tanθ=2
C. tanθ=21
D. tanθ=4
Solution
In this question, we are asked to find the angle θ that will produce maximum moment of the force about point A. For this, we will first find the equation for the moment of force about point A by considering horizontal and vertical component of applied force and then then for the maximum moment we equate the derivative of the equation with respect to θ with zero to find the angle θ .
Formula used:
τ=F×r,
Where, τ is moment of force, F is applied force and r is the perpendicular distance from the line of action of force to the point about which the moment is to be determined.
Complete step by step answer:
First of all, we have to consider the horizontal and vertical component of the applied force as shown in figure to find the equation for the moment about point A.
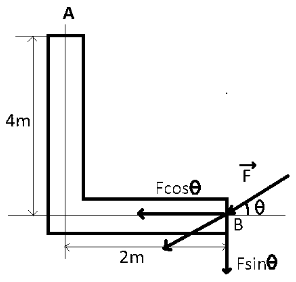
As shown in figure the horizontal component of the force is Fcosθ and the vertical component is Fsinθ. Both these components of force act in an anticlockwise direction towards point A.
Now let us take the moment of force about point A
τ=(Fcosθ×4)+(Fsinθ×2)
The value of force is given as 40N
Therefore,
τ=160cosθ+80sinθ
For the maximum moment, we will derive this equation with respect to θ and equate it to zero.
\dfrac{{d\tau }}{{d\theta }} = - 160\sin \theta + 80\cos \theta \\\
\Rightarrow 0 = - 160\sin \theta + 80\cos \theta \\\
\Rightarrow 160\sin \theta = 80\cos \theta \\\
\Rightarrow \dfrac{{\sin \theta }}{{\cos \theta }} = \dfrac{{80}}{{160}} \\\
\therefore \tan \theta = \dfrac{1}{2} \\\
Hence, option C is the right answer.
Note: We can also solve this problem by another method. We know that the moment of force is maximum when line of action of force is perpendicular to line AB. Therefore, if we redraw the diagram, it looks like:
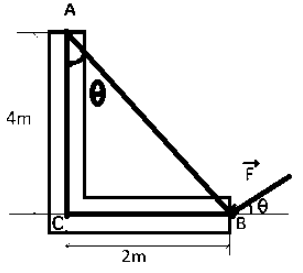
From the diagram, we can say that
\tan \theta = \dfrac{{BC}}{{AC}} \\\
\Rightarrow \tan \theta = \dfrac{2}{4} \\\
\Rightarrow \tan \theta = \dfrac{1}{2} \\\
\Rightarrow\tan \theta = \dfrac{{BC}}{{AC}} \\\
\Rightarrow \tan \theta = \dfrac{2}{4} \\\
\therefore \tan \theta = \dfrac{1}{2} \\\
