Question

A force of $15{\text{ N}}$ acts on a box as shown. What are the horizontal component and vertical component of the force?

A.Horizontal component, ${{\text{F}}_x}{\text{ = 7}}{\text{.5 N}}$
Vertical Component, ${{\text{F}}_y}{\text{ = 12}}{\text{.99 N}}$
B. Horizontal component, ${{\text{F}}_x}{\text{ = 7}}{\text{.5 N}}$
Vertical Component, ${{\text{F}}_y}{\text{ = 12}}{\text{.99 N}}$
C. Horizontal component, ${{\text{F}}_x}{\text{ = 7}}{\text{.5 N}}$
Vertical Component, ${{\text{F}}_y}{\text{ = 12}}{\text{.99 N}}$
D. Horizontal component, ${{\text{F}}_x}{\text{ = 7}}{\text{.5 N}}$
Vertical Component, ${{\text{F}}_y}{\text{ = 12}}{\text{.99 N}}$

Answer 1

Here the force acts at an angle of ${60^ \circ }$with positive direction of x-axis. The horizontal component of this force will be the force with force which is acting in only positive x-direction and vertical component is the only force which is acting in positive y-direction. We will split the force into both X and Y components respectively.

Formula Used:
For X-component:
${F_x}{\text{ = F cos}}\left( \theta \right)$
For Y-component:
${F_y}{\text{ = F sin}}\left( \theta \right)$
Here, ${F_x}$ and ${F_y}$ are the forces acting along x and y direction respectively. F is the magnitude of the force which is acting at angle $\theta$ with the positive direction of the x-axis.

Complete answer:
When we apply force horizontally on an object it means that we are applying force along x-direction. Similarly when we apply force vertically on an object, it means that we are applying force along y-direction. But when we apply force at angle $\theta$ with the positive direction of the x-axis it means that we are neither applying force in horizontal direction nor vertical direction. Then we have to make components of the force.

Similarly in the above question we have to find the components of the force, $F$. The horizontal component or x-component of force can be found by multiplying the force with the cosine of the angle between them. It can be written as,
${F_x}{\text{ = F cos}}\left( \theta \right)$
The vertical component or y-component of force can be found by multiplying the force with sine of angle between the force and positive direction of x-axis. It can be written as,
${F_y}{\text{ = F sin}}\left( \theta \right)$

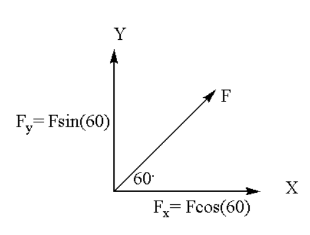
Here the angle between force and positive x-axis is ${60^ \circ }$ and the magnitude of force is $15{\text{ N}}$. Therefore its horizontal and vertical component would be:
$\Rightarrow {\text{ }}{F_x}{\text{ = F cos}}\left( \theta \right)$
$\Rightarrow {\text{ }}{F_x}{\text{ = 15 }} \times {\text{ cos}}\left( {60} \right)$
$\Rightarrow {\text{ }}{F_x}{\text{ = 15 }} \times {\text{ }}\dfrac{1}{2}$
$\Rightarrow {\text{ }}{F_x}{\text{ = 7}}{\text{.5 N}}$
Similarly for vertical component:
$\Rightarrow {\text{ }}{F_y}{\text{ = F sin}}\left( \theta \right)$
$\Rightarrow {\text{ }}{F_y}{\text{ = 15 }} \times {\text{ sin}}\left( {60} \right)$
$\Rightarrow {\text{ }}{F_y}{\text{ = 15 }} \times {\text{ }}\dfrac{{\sqrt 3 }}{2}$
$\therefore {\text{ }}{F_y}{\text{ = 12}}{\text{.99 N}}$
Hence the horizontal and vertical components of force are $7.5{\text{ N}}$ and $12.99{\text{ N}}$.

Therefore the correct option is B.

Note: For finding vertical components the angle which we used must be the angle between the force and positive x-axis. We can find components of only vector quantities because they have direction and magnitude both. When force acts at an angle on an object then the motion of the object is not a linear motion in x or y direction only.