Question

A force of 100N is applied on a block of mass 3 kg as shown in the figure. The coefficient of friction between the surface of the block is $\dfrac {1}{4}$. The friction force acting on the block is

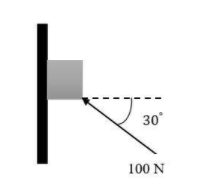
A.20 N downwards
B.25 N upwards
C.15 N downwards
D.20 N upwards

Answer 1

Frictional force can be defined as the force which is produced by two surfaces when they come in contact to each other and slide against each other. To solve this problem, use the formula for frictional force as the value of coefficient of friction is given. However, we have to calculate the normal force. So, using the given value for applied force and angle of friction, calculate the normal force. Then, substitute these values in frictional force and calculate the friction force acting on the block.

Complete answer:
Given: Applied Force (F)= 100 N
Mass (m)= 3kg
Angle of friction ${(\theta)}= 30°$
Frictional force is given by,
${F}_{\mu}= \mu \times N$ …(1)
Where, N is the normal force
$\mu$ is the coefficient of friction
But, $N= F \cos {\theta}$
Substituting the values in above equation we get,
$N= 100 \times \cos{30°}$
$\Rightarrow N= 100 \times \dfrac {\sqrt {3}}{2}$
$\Rightarrow N= 86.60 N$
Now, substituting values in the equation. (1) we get,
${F}_{\mu}= \dfrac {1}{4} \times 86.60$
$\therefore {F}_{\mu}= 21.65 N$
Thus, the friction force acting on the block is approximately 20 N downwards.

Hence, the correct answer is option A i.e. 20 N downwards.

Note:
Remember that the friction force or force of friction can never be greater than the applied force. Whenever the applied force is less than the friction force, the friction force adjusts itself so that it is less as compared to the applied force. Friction force is dependent on the object’s angle and location. The direction of force and friction force are always in opposite directions.