Question

A force is applied on a body of mass 20kg moving with the velocity of 40m/s. the body attains a velocity of 50m/s in 2 seconds. Calculate the work done by the body.

Answer 1

Use work energy theorem according to which work done by the body is equal to change in kinetic energy The net change in kinetic energy can be calculated by the difference between final and initial kinetic energies.

Formula used:
$K.E = \dfrac{1}{2}m{v^2}$

Complete step by step solution:
The given problem can be visualized with the following diagram:

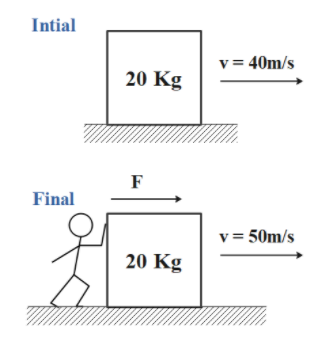
We know that the work energy theorem states that the net work done by the forces on an object is equal to the change in kinetic energy of the object. Mathematically,
$W = \Delta K.E$
Where, ‘W’ is the work done by the object and ‘K.E’ is the kinetic energy of the object. The net change in kinetic energy is given by, $\Delta K.E = {\left( {K.E} \right)_{{\text{final}}}} - {\left( {K.E} \right)_{{\text{initial}}}}$
This is the difference of final kinetic energy and initial kinetic energy. Now we have to calculate final and initial kinetic energies. For initial kinetic energy, mass = 20kg, velocity = 40m/s.
As we know that, $K.E = \dfrac{1}{2}m{v^2}$
Where ‘m’ is the mass of the object and ‘v’ is the velocity of the object.
\eqalign{ & {\left( {K.E} \right)_{{\text{initial}}}} = \dfrac{1}{2} \times 20 \times {\left( {40} \right)^2} \cr & \Rightarrow {\left( {K.E} \right)_{{\text{initial}}}} = 10 \times 1600 \cr & \therefore {\left( {K.E} \right)_{{\text{initial}}}} = 16 \times {10^3}J \cr}
Now for the final kinetic energy, mass = 20kg, velocity = 50m/s.
\eqalign{ & {\left( {K.E} \right)_{{\text{final}}}} = \dfrac{1}{2} \times 20 \times {\left( {50} \right)^2} \cr & \Rightarrow {\left( {K.E} \right)_{{\text{final}}}} = 10 \times 2500 \cr & \therefore {\left( {K.E} \right)_{{\text{final}}}} = 25 \times {10^3}J \cr}
The change in the kinetic energy will be given by the difference of the final kinetic energy and the initial kinetic. Mathematically, we have:
\eqalign{ & \Delta K.E = {\left( {K.E.} \right)_{{\text{final}}}} - {\left( {K.E.} \right)_{Initial}} \cr & \Rightarrow 2\Delta K.E = 5 \times {10^3} - 16 \times {10^3} \cr & \therefore \Delta K.E = 9 \times {10^3}J \cr}
Considering as per the work – energy theorem. We can equate the change in kinetic energy to the work done by the body. So we have:
$W = \Delta K.E = 9 \times {10^3}J$

Therefore the work done by the body is $9 \times {10^3}$ J or 9000 joule.

Note:
Kinetic energy is the energy an object has because of its motion. If we want to accelerate an object, then we must apply a force. Applying force requires us to do work. After work is done energy has been transferred to the object, and the object will be moving with a new constant speed.