Question

A force acts for 0.2 seconds on an object having mass 1.4 kg initially at rest. The force stops to act but the object moves through 4 m in the next 2 seconds. Find the magnitude of the force.
A) 11N
B) 19N
C) 14N
D) 21N

Answer 1

We need to understand the relation between the force applied on a body of certain mass the duration of the force application with the velocity attained by the body which can be used to move the body without any force to solve this problem.

Complete step by step solution:
We are given a body of certain mass which was at rest initially and applied a force F. It is said that the force acted on the body for a certain amount of time and then the force application is stopped.
We know that according to Newton's second law of motion, the body will continue to be the motion at which the force application was stopped given that the body experiences no external forces.

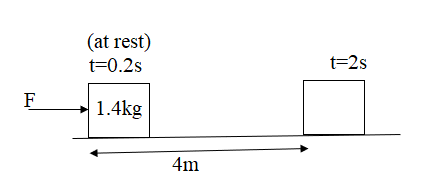
We are given the distance travelled by the object after the force is removed and also the time taken for that motion. From this data we can find the maximum velocity attained by the body due to the force as –

& v=\dfrac{\text{Distance}}{\text{Time}} \\\ & \Rightarrow v=\dfrac{4m}{2s} \\\ & \therefore v=2m{{s}^{-1}} \\\ \end{aligned}$$ Now, we can calculate the applied force using the relation between the force, the momentum change of the body and the time duration which is given as – $$\begin{aligned} & F=\dfrac{\Delta p}{t} \\\ & \Rightarrow F=\dfrac{m\Delta v}{t} \\\ & \Rightarrow F=\dfrac{m(v-u)}{t} \\\ & \Rightarrow F=\dfrac{(1.4kg)(2m{{s}^{-1}}-0)}{0.2s} \\\ & \therefore F=14N \\\ \end{aligned}$$ So, we get the force applied on the body for the duration of 0.2 seconds as 14 N. **Hence, the correct answer is option C.** **Note:** The force can also be found after finding the acceleration of the body which can be found as the rate of change in the initial and final velocities of the body after the application of the force. Both will give us the same solution irrespective of the method.