Question
Question: A follows parallel path first order reactions giving B and C as, if the initial concentration of A i...
A follows parallel path first order reactions giving B and C as, if the initial concentration of A is 0.25 M , the concentration of C after 5 hours of reaction is:
[λ1=1.5×10−5s−1,λ2=5×10−6s−1]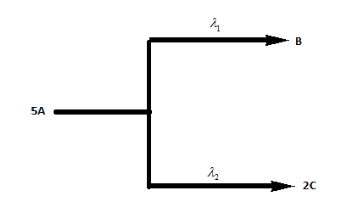
A.7.56×10−3 M
B.6.62×10−3 M
C.9.36×10−3 M
D.None of these
Solution
In this question, we shall first calculate the amount of A left in the mixture after 5 hours. The rate constant of decomposition of A will be the sum of both the rate constants. Then, we shall calculate the amount of A decomposed during the given time. At the end, we shall calculate the concentration of C formed using stoichiometric ratios of the reaction.
Formula used: Integrated rate of reaction of first order:
2.303log[A]t[A]0=λ×t where [A]0 is the initial concentration, [A]t is the concentration at time t, λ is the rate constant and t is the time completed.
Complete step by step answer:
As we know that, the reaction is occurring in two parallel paths with different rate constants of formation of both the compounds. But, with respect to A, the rate constant will be the sum of the both the rate constants.
λT=λ1+λ2
λT=15×10−6+5×10−6=20×10−6
Substituting the appropriate values in their correct units in the integrated rate equation we get:
2.303log[A]t0.25=20×10−6×5×60×60
Solving this for [A]t , we get:
log[A]t0.25=2.3030.36
⇒log[A]t=log0.25−0.156
Solving this, we get:
[A]t=0.1744 M
So, from here, we shall calculate the amount of A which was decomposed during the reaction:
[A]decomp=[A]0−[A]t
[A]decomp=0.25−0.1744=0.0756 M
The rate equation of A to C will be:
5[A]λ12[C]
Now, according to the reaction, 5 moles of A will decompose to form 2 moles of C at a rate constant of λ2 . So, the amount of C formed shall be:
[C]=[λ1+λ2λ2]×[A]decomp×52 (Eq. 1)
⇒[C]=[20×10−65×10−6]×0.0756×52
Solving this, we shall get:
[C]=7.56×10−3 M
∴ The correct option is option A, i.e. 7.56×10−3 M
Note:
In this question, in Eq. 1 as 5 moles of A forms 2 moles of C, this means that 1 mole of A will form 52 moles of C. As the total rate of decomposition of A is λT , so for the formation of only C, the rate constant λ2 is divided by λT .
