Question

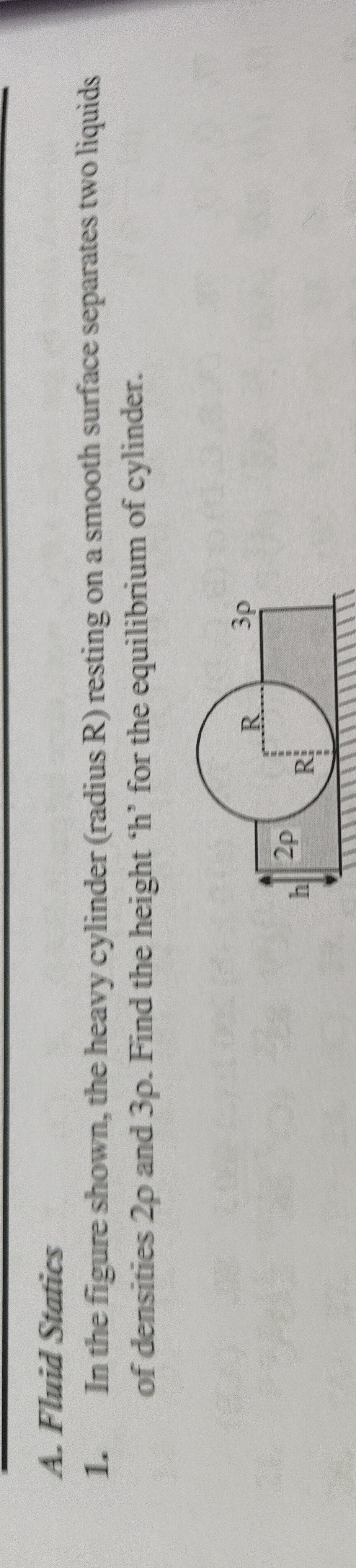
In the figure shown, the heavy cylinder (radius R) resting on a smooth surface separates two liquids of densities 2p and 3p. Find the height 'h' for the equilibrium of cylinder.

Answer 1

The problem statement is incomplete as the weight of the cylinder or its dimensions are not provided, which are necessary to solve for the equilibrium height 'h'.

Answer 2

To find the height 'h' for the equilibrium of the cylinder, we need to equate the buoyant forces acting on the cylinder to its weight. Let $W$ be the weight of the cylinder. The cylinder is partially submerged in a liquid of density $2\rho$ up to height $h$, and it is also in contact with a liquid of density $3\rho$.

The buoyant force due to the liquid of density $2\rho$ is $F_{B1} = (2\rho) g V_1$, where $V_1$ is the volume of the cylinder submerged in this liquid. The buoyant force due to the liquid of density $3\rho$ is $F_{B2} = (3\rho) g V_2$, where $V_2$ is the volume of the cylinder submerged in this liquid.

For equilibrium, the sum of the buoyant forces must balance the weight of the cylinder: $W = F_{B1} + F_{B2}$ $W = (2\rho) g V_1 + (3\rho) g V_2$

From the figure, it is implied that the cylinder is partially submerged in the lower liquid (density $2\rho$) up to a height $h$. The upper liquid (density $3\rho$) is above this. The problem statement mentions the cylinder is "resting on a smooth surface" and "separates two liquids". This phrasing is somewhat ambiguous. If the cylinder is resting on a surface at the bottom, then the lower liquid is $2\rho$ and the upper liquid is $3\rho$. If the cylinder is floating, then the weight must be balanced by the buoyant forces.

Assuming the cylinder is floating and partially submerged in the liquid of density $2\rho$ up to height $h$, and the liquid of density $3\rho$ is above it. The volume submerged in the lower liquid is $V_1$. The volume submerged in the upper liquid is $V_2$. The total submerged volume is $V_{submerged} = V_1 + V_2$.

However, without the weight of the cylinder ($W$) or its total height and density, we cannot determine the specific value of $h$. The problem statement is incomplete.