Question
Question: A fluid of density $\rho$ and coefficient of viscosity $\eta$ is flowing in a tube of length $l$ and...
A fluid of density ρ and coefficient of viscosity η is flowing in a tube of length l and radius R. Flow of the fluid is steady. Velocity v of the flow is given by v=v0(1−R2r2), where r is distance of flowing fluid from axis.
The difference of pressure at ends of the tube is
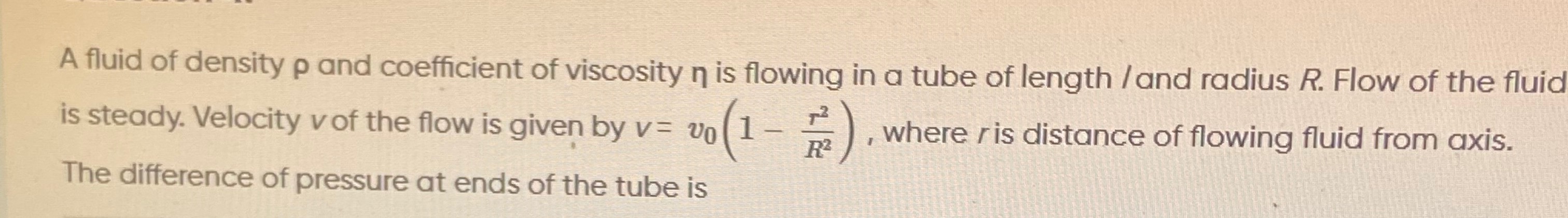
ΔP=R24ηv0l
Solution
We start with the known result for viscous flow in a tube. For steady, incompressible, laminar flow the Navier–Stokes equation in a tube gives the velocity profile as
v(r)=−4η1dxdp(R2−r2)
Comparing with the given profile
v(r)=v0(1−R2r2)=v0R2R2−r2,
we equate the two coefficients (the factor multiplying (R2−r2)):
4η−1dxdp=R2v0.
Solving for dxdp we have:
dxdp=−R24ηv0.
Over a tube of length l the pressure difference is
ΔP=P1−P2=−dxdpl=R24ηv0l.
Thus, the difference of pressure at the ends of the tube is
ΔP=R24ηv0l.
Core Explanation:
- Compare the given velocity profile with the standard parabolic profile.
- Equate coefficients to get dxdp=−R24ηv0.
- Multiply by the tube length l to obtain ΔP=R24ηv0l.
