Question
Question: A fluid container containing a liquid density p is accelerating upwards with acceleration along the ...
A fluid container containing a liquid density p is accelerating upwards with acceleration along the inclined plane of inclination α as shown. Then the angle of inclination θ of free surface is:
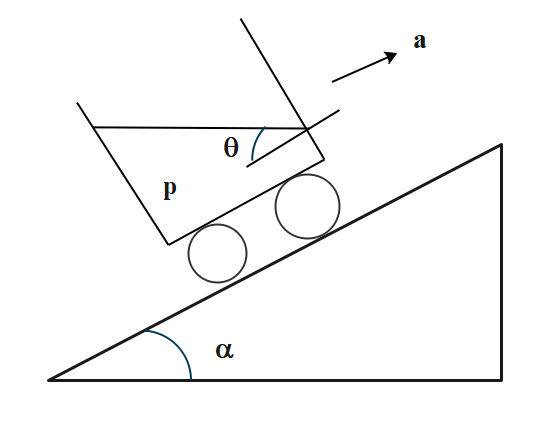
Solution
A fluid container containing a liquid is accelerating upwards with an acceleration along the inclined plane of inclination. Deduce the components of forces acting on the container with the help of the given figure. Then find the angle of inclination of the free surface by finding the net force acting on the container.
Complete step by step answer:
We will recreate a rough diagram representing the given system and form components of the forces acting on it then balance them out.
A pseudo force is defined as the apparent force that acts on all masses whose motion is described using non- non-inertial frame of reference. When a frame of reference starts accelerating compared to a non- accelerating frame then pseudo force comes in effect. Applying pseudo force on a particle of mass m.
Recreating the diagram with the components of forces acting on it we get the following diagram:
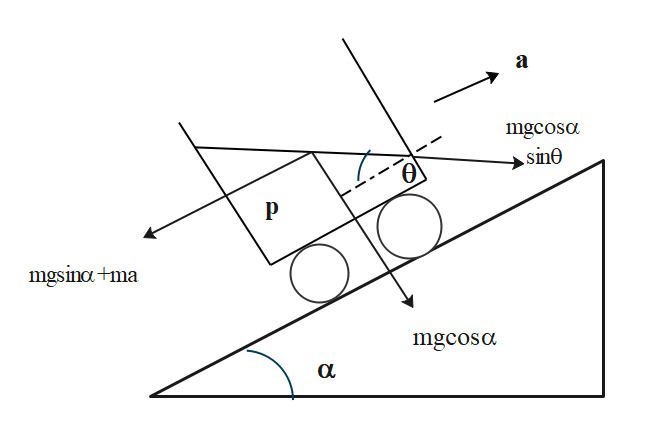
macosθ=mgcos[90−(θ−α)]
⇒gacosθ=gsin(θ−α)
⇒ga=cosθsinθcosα−cosθcosθsinα
⇒tanθ=cosαga+sinα=gcosαa+gsinα
⇒θ=tan−1gcosαa+gsinα
Hence, Then the angle of inclination θ of free surface is tan−1gcosαa+gsinα
Note:
The net force acting on a body is defined as the vector sum of the forces acting on the body or a particle. Net force is a single force that replaces the effect of the original forces on the body’s motion. It provides the particle the same acceleration which is given by all those actual forces together. The relation between the acceleration of an object down an incline is directly proportional to the sine of the angle of incline as the relationship is linear and passes through the origin.
