Question

A floral design on a floor is made up of 16 tiles which are triangular, the sides of the triangle being 9cm, 28cm and 35cm. Find the cost of polishing the tiles at the rate of 50p per $c{m^2}$.

Answer 1

Hint: In this question find the area of the triangular shaped tile using the formula $A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)}$, where s is half the perimeter of triangle. Multiply this area with cost per $c{m^2}$ to get the answer.

Complete step-by-step answer:

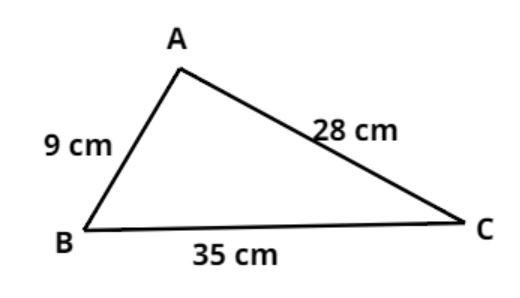
The pictorial representation of one tile is shown above.
Let a = 9 cm, b= 28 cm and c = 35 cm where a, b and c are the sides of the triangle respectively.

As we know that the area (A) of the triangle in terms of its sides is given as
$\Rightarrow A = \sqrt {s\left( {s - a} \right)\left( {s - b} \right)\left( {s - c} \right)}$
Where (s) is the half of the perimeter of the triangle.
As we know that the perimeter is the sum of all the sides.
$\Rightarrow s = \dfrac{{a + b + c}}{2} = \dfrac{{9 + 28 + 35}}{2} = \dfrac{{72}}{2} = 36$

Now calculate the area of the triangle
$\Rightarrow A = \sqrt {36\left( {36 - 9} \right)\left( {36 - 28} \right)\left( {36 - 35} \right)} = \sqrt {36\left( {27} \right)\left( 8 \right)\left( 1 \right)} = 36\sqrt 6$ $cm^2$.
Now it is given that there are a total of 16 tiles to make a floor.
So the area of 16 tiles = $16 \times 36\sqrt 6 = 576\sqrt 6$ $cm^2$.
Now it is given that the cost of polishing the tiles at the rate of 50p per $cm^2$.
As we know 50p = (1/2) Rs.
So the cost of $576\sqrt 6$ $cm^2$ = $\dfrac{1}{2} \times 576\sqrt 6 = 288\sqrt 6 = 288 \times 2.45 = 705.45$ Rs. $\left[ {\because \sqrt 6 = 2.45} \right]$
So the cost of polishing the tiles is Rs. 705.45.
So this is the required answer.

Note: The perimeter of a triangle is the sum of all the sides, that’s how half of the perimeter is being calculated, it is advised to remember this form of area of triangle as well. Another method to find the area would be to use the concept of $\dfrac{1}{2} \times base \times height$, but calculation of height would have been a tricky part, hence this method is preferred.