Solveeit Logo
Login

Question

Question: A floor wiper makes an angle (90−\(\theta \)) with horizontal floor​ \({\mu _n}\)and \({\mu _k}\)are...

A floor wiper makes an angle (90−θ\theta ) with horizontal floor​ μn{\mu _n}and μk{\mu _k}are coefficients of static and kinetic frictions between the wiper and the floor. The wiper cannot be used to wipe the floor for θ\theta >θ0{\theta _0} even if a large force directed along the handle aiming towards the center is applied. Angle ​θ0{\theta _0} is given by:-

Explanation

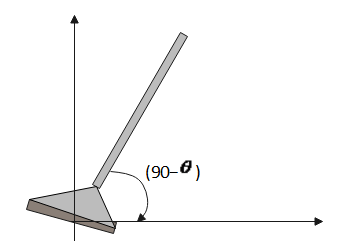
Solution

In this question, we will use the relation between forces applied. Further, by solving this equation, for the given angle, we will get the required result. Further, we will study the basics of friction force and its types, for our better understanding.
Formula used:
mg+Fcos⁡θ=Rmg + F\cos \theta = R
Fsin⁡θ−μR⩾0F\sin \theta - \mu R \geqslant 0

Complete step-by-step solution
As we know, there are different forces acting on an object, as shown in the free body diagram below:

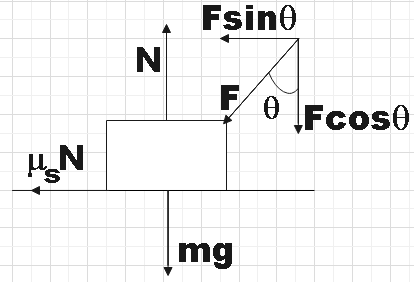
We could now balance the forces acting in the vertical directions considering the fact that there is no vertical displacement.
mg+Fcos⁡θ=Nmg+F\cos \theta =N………………………………………… (1)
Here, m is the mass of the given wiper, F is the applied force on the wiper towards the centre and N is the normal reaction of ground upward.
The condition for the motion to occur could be given by,
Fsin⁡θ−μsN≥0F\sin \theta -{{\mu }_{s}}N\ge 0
Now, substituting the value of N from (1), we get:
Fsin⁡θ−μs(mg+Fcos⁡θ)≥0F\sin \theta -{{\mu }_{s}}(mg+F\cos \theta )\ge 0
⇒sin⁡θ−μscos⁡θ≥μsmgF\Rightarrow \sin \theta -{{\mu }_{s}}\cos \theta \ge \dfrac{{{\mu }_{s}}mg}{F}
We see that all the quantities on the right hand side of the inequality sign are positive, so, we could rewrite the equation as,
⇒sin⁡θ−μscos⁡θ≥0\Rightarrow \sin \theta -{{\mu }_{s}}\cos \theta \ge 0
⇒−μscos⁡θ≥−sin⁡θ\Rightarrow -{{\mu }_{s}}\cos \theta \ge -\sin \theta
⇒tan⁡θ≥μs\Rightarrow \tan \theta \ge {{\mu }_{s}}
For the limiting case we have:
tan⁡θ0≥μ0\tan {{\theta }_{0}}\ge {{\mu }_{0}}
∴θ0≥tan⁡−1μ0\therefore {{\theta }_{0}}\ge {{\tan }^{-1}}{{\mu }_{0}}
Therefore, we got the required angle.
Additional information:
As we know, the frictional force can be defined as the force exerted by a surface when an object moves across it or even when the object makes an effort to move across the surface. Also, there are generally three types of frictional force, namely- static friction, sliding friction, and rolling friction. So, we can say that the friction force often opposes the motion of an object.
Now, sliding friction is the friction that comes into action when any object is sliding over another surface. Here, we know that the sliding friction is weaker than the static friction.

Note: We should remember that frictional force is a force that opposes the motion of any object or body. We should also remember one important point that there are various kinds of lubricants that are used to overcome the frictional force for example- grease, oil etc.