Question

A flexible chain of weight W hangs between two fixed positions A and B which are at the same horizontal level. The inclination of the chain with the horizontal at both the points of support is $\theta$. What is the tension in the chain at the midpoint?

$\begin{aligned} & (A)\dfrac{W}{2}\cos ec\theta \\\ & (B)\dfrac{W}{2}\tan \theta \\\ & (C)\dfrac{W}{2}\cot \theta \\\ & (D)None \\\ \end{aligned}$

Answer 1

Since, the chain is at rest, then it means the net force on the chain is equal to zero. And, also the tension in the chain should be uniform at all parts of the chain. We will use this analysis to derive the horizontal and vertical component of this tension and balance them out in their respective directions with all the other given force to get our required solution.

Complete answer:
Let us first understand the force acting on the chain with the help of the following diagram:

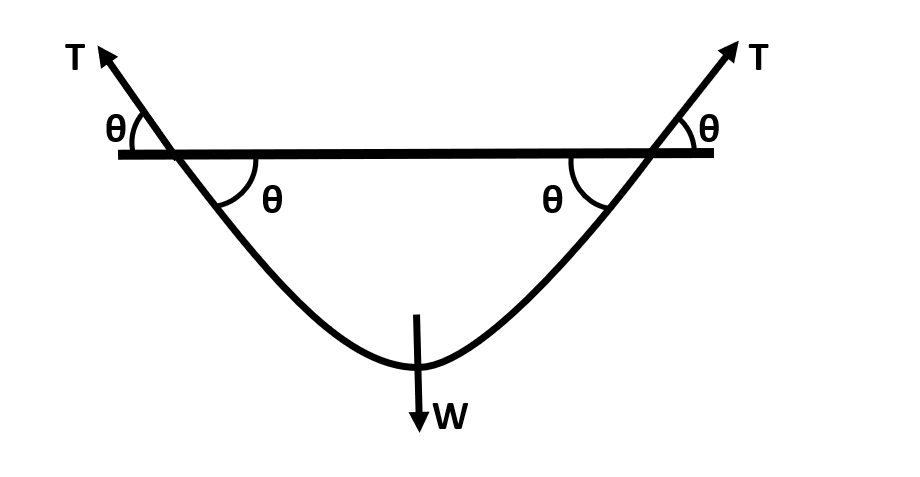
Let the force acting on the two ends of the chain at the point of support be equal to T. Then, these tensions will make an angle of $\theta$ with the horizontal as opposite angles are equal. And the other force acting on the chain in the vertical direction is the force of gravity due to its own weight which is given by W.
Now, balancing the forces in the horizontal direction, we get:
$\Rightarrow T\cos \theta -T\cos \theta =0$
Which indicates that the horizontal component of the hinge force is balanced equally in the opposite direction.
Now, since this hinge force is equal to the tension in the string in vertical direction, the tension in the string at the midpoint can be calculated by equating the net force on it in vertical direction. Mathematically, this can be written as:
$\begin{aligned} & \Rightarrow T\sin \theta +T\sin \theta -W=0 \\\ & \Rightarrow 2T\sin \theta =W \\\ & \Rightarrow T=\dfrac{W}{2\sin \theta } \\\ & \therefore T=\dfrac{W}{2}\cos ec\theta \\\ \end{aligned}$
Hence, the tension at the midpoint of the string comes out to be $\dfrac{W}{2}\cos ec\theta$ .
So, the correct answer is “Option A”.

Note: The net force on the string is due to the support and it is equal to the tension in the string. This is the reason why we calculated the horizontal component of this force on the chain and commented on the tension in the string horizontally at the midpoint.