Question

A flashlight cell of emf $1 \cdot 5{\text{volts}}$ gives $15{\text{A}}$ current when connected to an ammeter of resistance $0 \cdot 04\Omega$. Find the internal resistance of the cell.
A) $0 \cdot 04\Omega$
B) $0 \cdot 06\Omega$
C) $0 \cdot 10\Omega$
D) $10\Omega$

Answer 1

Here the cell is connected directly to an ammeter. So the internal resistance of the flashlight cell and that of the ammeter will form a series connection. Ohm’s law gives the effective resistance of the circuit to be directly proportional to the voltage and inversely proportional to the current in the circuit.

Formulas used:
-The effective resistance of two resistors in series is given by, ${R_{eff}} = R + r$ where $R$ and $r$ are the resistances of two resistors in series.
-The effective resistance of a circuit as per Ohm’s law is given by, ${R_{eff}} = \dfrac{V}{I}$ where $V$ is the voltage across the circuit and $I$ is the current in the circuit.

Complete step by step answer.
Step 1: Sketch a circuit diagram depicting the above mentioned setup and list the parameters provided in the question.

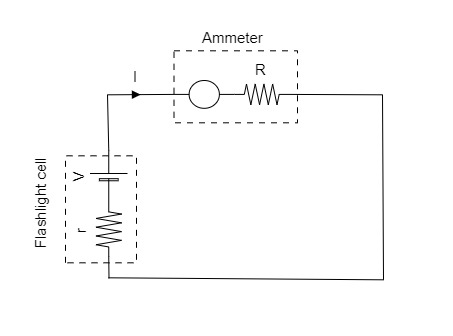
The emf or voltage of the cell is given to be $V = 1 \cdot 5{\text{V}}$ .
The current in the circuit is given to be $I = 15{\text{A}}$ .
The resistance of the ammeter is given to be $R = 0 \cdot 04\Omega$ .
Step 2: Express the effective resistance of the circuit.
As the internal resistance $r$ of the cell and the resistance of the ammeter are connected in series, the effective resistance of the circuit can be expressed as ${R_{eff}} = R + r$ ------- (1)
Substituting for $R = 0 \cdot 04\Omega$ in equation (1) we get, ${R_{eff}} = 0 \cdot 04 + r$ .
Thus the effective resistance of the circuit is ${R_{eff}} = 0 \cdot 04 + r$ .
Step 3: Based on Ohm’s law, express the effective resistance of the given circuit.
According to Ohm’s law, the effective resistance of the given circuit can be expressed as
${R_{eff}} = \dfrac{V}{I}$ ----------- (2)
Substituting for ${R_{eff}} = 0 \cdot 04 + r$, $V = 1 \cdot 5{\text{V}}$ and $I = 15{\text{A}}$ in equation (2) we get, $0 \cdot 04 + r = \dfrac{{1 \cdot 5}}{{15}}$
$\Rightarrow r = 0 \cdot 1 - 0 \cdot 04 = 0 \cdot 06\Omega$ .
Thus the internal resistance of the flashlight cell is $r = 0 \cdot 06\Omega$ .

So the correct option is B.

Note: An ammeter is always connected in series with the device of whose current is to be recorded. Here the current through the flashlight cell is given and so the ammeter is connected in series with the cell. A series connection of resistors is obtained when one of the ends of each resistor are connected together. In our sketched circuit diagram, we see that only one end of both resistors $R$ and $r$ are connected together.