Question

A flagstaff stands vertically on a pillar, the height of the flagstaff being double the height of the pillar. A man on the ground at a distance finds that both the pillar and the flagstaff subtend equal angles at his eyes. The ratio of the height of the pillar and the distance of the man from the pillar, is
(a) $\sqrt{3}:1$
(b) 1:3
(c) $1:\sqrt{3}$
(d) $\sqrt{3}:2$

Answer 1

Hint : First, before proceeding for this, we must suppose all the values to construct a figure in which AB is the height of the flagstaff and BC is the height of the pillar with height as h and x be the distance between the man and the pillar and man is making an angle of $\theta$ with the height of the pillar and it has the same angle with the height of the flagstaff. Then, by applying the trigonometric properties as the tangent of the angle is the ratio of the perpendicular to the base. Then, solve the above expression to get the value of the ratio of the height of the pillar and the distance of the man from the pillar.

Complete step-by-step answer :
In this question, we are supposed to find the ratio of the height of the pillar and the distance of the man from the pillar.
So, before proceeding for this, we must suppose all the values to construct a figure in which AB is the height of the flagstaff and BC is the height of the pillar with height as h and x be the distance between the man and the pillar and man is making an angle of $\theta$ with the height of the pillar and it has the same angle with the height of the flagstaff.
Then, by using the above conditions, the figure is as:

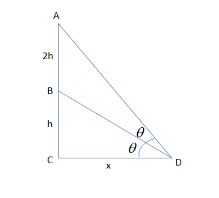
Now, from the figure AB=2h and BC=h.
So, in $\Delta ADC$ , by applying the trigonometric properties as the tangent of the angle is the ratio of the perpendicular to the base as:
$\begin{aligned} & \tan 2\theta =\dfrac{AC}{CD} \\\ & \Rightarrow \tan 2\theta =\dfrac{3h}{x} \\\ \end{aligned}$
Now, by again using the same property in the $\Delta BCD$ as:
$\tan \theta =\dfrac{h}{x}$
Now, we know the basic formula as:
$\tan 2\theta =\dfrac{2\tan \theta }{1-{{\tan }^{2}}\theta }$
Now, by substituting the value of $\tan 2\theta$ in the above equation as:
$\dfrac{2\tan \theta }{1-{{\tan }^{2}}\theta }=\dfrac{3h}{x}$
Now, we get value of $\tan \theta$ from the $\Delta BCD$ and then substituting in the above equation, we get:
$\dfrac{2\left( \dfrac{h}{x} \right)}{1-{{\left( \dfrac{h}{x} \right)}^{2}}}=\dfrac{3h}{x}$
Now, solve the above expression to get the value of the ratio of the height of the pillar and the distance of the man from the pillar as:
$\begin{aligned} & 2=3\left[ 1-{{\left( \dfrac{h}{x} \right)}^{2}} \right] \\\ & \Rightarrow 2=3-3{{\left( \dfrac{h}{x} \right)}^{2}} \\\ & \Rightarrow 3{{\left( \dfrac{h}{x} \right)}^{2}}=1 \\\ & \Rightarrow {{\left( \dfrac{h}{x} \right)}^{2}}=\dfrac{1}{3} \\\ & \Rightarrow \dfrac{h}{x}=\dfrac{1}{\sqrt{3}} \\\ \end{aligned}$
So, the ratio of the height of the pillar and the distance of the man from the pillar is $1:\sqrt{3}$ .
So, the correct answer is “Option C”.

Note : Now, to solve these types of questions we need to know some of the basic trigonometric calculations of the angles from the right angles triangle. So, the basic calculation formulas are as:
$\tan \theta =\dfrac{P}{B}$ where P is perpendicular and B is base.
$\sin \theta =\dfrac{P}{H}$ where P is perpendicular and H is hypotenuse.
$\cos \theta =\dfrac{B}{H}$ where B is base and H is hypotenuse.