Question

A flagstaff on the top of tower 80m high subtends an angle ${\tan ^{ - 1}}\left( {\dfrac{1}{9}} \right)$ at a point on the ground which is 100m from the foot of the tower. The height of the flagstaff is
A. 40m
B. 30m
C. 20m
D. $\dfrac{{100}}{{\sqrt 2 }}m$

Answer 1

Hint : A flagstaff is another term for a flagpole. The flagpole is on the top of the tower. Height of the tower is given. The flagpole subtends an angle of ${\tan ^{ - 1}}\left( {\dfrac{1}{9}} \right)$ with the ground which is 100m away from the tower. Draw the diagram of this scenario. Tangent of the angle will be $\dfrac{1}{9}$ , write the tangent as the ratio of opposite side and adjacent side to the angle. Use this info to find the height of the flagpole.

Complete step-by-step answer :
We are given that a flagstaff on the top of tower 80m high subtends an angle ${\tan ^{ - 1}}\left( {\dfrac{1}{9}} \right)$ at a point on the ground which is 100m from the foot of the tower.
We have to find the height of the flagstaff (flagpole).
Let the height of the flagpole be x m.

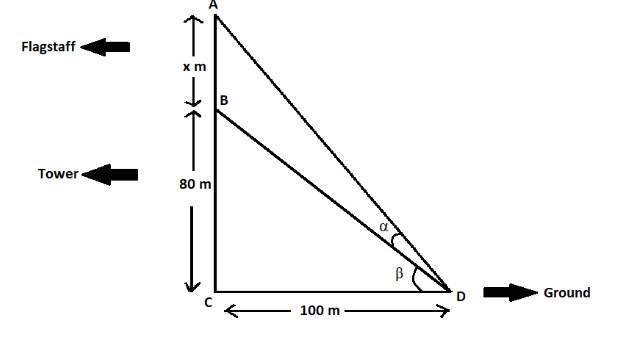
The angle $\alpha$ is ${\tan ^{ - 1}}\left( {\dfrac{1}{9}} \right)$ . This means
$\alpha = {\tan ^{ - 1}}\left( {\dfrac{1}{9}} \right) \\\ \Rightarrow \tan \alpha = \dfrac{1}{9} \\\$
Tangent of angle β is the ratio of side BC (tower) and side CD.
$\tan \beta = \dfrac{{BC}}{{CD}} \\\ BC = 80m,CD = 100m \\\ \Rightarrow \tan \beta = \dfrac{{80}}{{100}} = \dfrac{4}{5} \\\$
Tangent of angle $\left( {\alpha + \beta } \right)$ is the ratio of AB+BC (tower + flagpole) and side CD.
$\tan \left( {\alpha + \beta } \right) = \dfrac{{AB + BC}}{{CD}} \\\ AB = xm,BC = 80m,CD = 100m \\\ \Rightarrow \tan \left( {\alpha + \beta } \right) = \dfrac{{x + 80}}{{100}} \\\$
We know that the value of $\tan \left( {a + b} \right) = \dfrac{{\tan a + \tan b}}{{1 - \tan a.\tan b}}$
$\Rightarrow \tan \left( {\alpha + \beta } \right) = \dfrac{{\tan \alpha + \tan \beta }}{{1 - \tan \alpha .\tan \beta }} \\\ \tan \left( {\alpha + \beta } \right) = \dfrac{{x + 80}}{{100}},\tan \alpha = \dfrac{1}{9},\tan \beta = \dfrac{4}{5} \\\ \Rightarrow \dfrac{{x + 80}}{{100}} = \dfrac{{\left( {\dfrac{1}{9}} \right) + \left( {\dfrac{4}{5}} \right)}}{{1 - \left( {\dfrac{1}{9}} \right)\left( {\dfrac{4}{5}} \right)}} \\\ \Rightarrow \dfrac{{x + 80}}{{100}} = \dfrac{{\left( {\dfrac{{5 + 36}}{{45}}} \right)}}{{1 - \left( {\dfrac{4}{{45}}} \right)}} = \dfrac{{\left( {\dfrac{{5 + 36}}{{45}}} \right)}}{{\left( {\dfrac{{45 - 4}}{{45}}} \right)}} \\\ \Rightarrow \dfrac{{x + 80}}{{100}} = \dfrac{{\left( {\dfrac{{41}}{{45}}} \right)}}{{\left( {\dfrac{{41}}{{45}}} \right)}} = 1 \\\ \Rightarrow x + 80 = 100 \\\ \Rightarrow x = 100 - 80 \\\ \therefore x = 20m \\\$
The height of the flagpole (flagstaff) is 20m.

So, the correct answer is “Option C”.

Note : In the above solution, the angles made by the flagpole and the tower with the ground away from the tower are termed as angle of elevation. The upwards angle from the horizontal to line of sight from an object is the angle of elevation whereas the downwards angle from the horizontal to the object is the angle of depression. Do not confuse the angle of elevation with the angle of depression.