Question

A flag post stands on the top of a building. From a point on the ground, the angles of elevation
of the top and the bottom of the flag post are ${60^0}$ and ${45^0}$ respectively. If the height of the flag post is $10m$, find the height of the building. $\left( {\sqrt 3 = 1.732} \right)$

Answer 1

Hint: Draw the figure and use trigonometric formulas to solve.

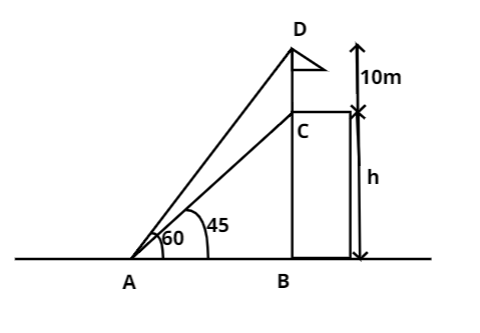
Le A be the point of observation and B be the foot of the building.
Let BC denote the height of the building and CD denote height of the flag post.
Given that $\angle CAB = {45^ \circ },{\text{ }}\angle DAB = {60^ \circ }{\text{ and }}CD = 10m$
Let $BC = h{\text{ metres}}$ and $AB = x{\text{ metres}}$.
Now in the right angled $\Delta CAB$,
$\tan {45^ \circ } = \dfrac{{BC}}{{AB}}$
Thus, AB =BC i.e. $x = h$ -Equation(1)
Also, in right angled $\Delta DAB$,

$${\text{tan6}}{{\text{0}}^ \circ }{\text{ = }}\dfrac{{BD}}{{AB}} \\\ \Rightarrow AB = \dfrac{{h + 10}}{{\tan {{60}^ \circ }}} \\\$$

$\Rightarrow {\text{ }}x = \dfrac{{h + 10}}{{\sqrt 3 }}$ -Equation (2)
From Equation (1) and Equation (2) we get,

$$h = \dfrac{{h + 10}}{{\sqrt 3 }} \\\ \Rightarrow \sqrt 3 h - h = 10 \\\ \Rightarrow h = \left( {\dfrac{{10}}{{\sqrt 3 - 1}}} \right) \\\$$

Now, when we rationalize it we get,

$$h = \left( {\dfrac{{10}}{{\sqrt 3 - 1}}} \right)\left( {\dfrac{{\sqrt 3 + 1}}{{\sqrt 3 + 1}}} \right) = \dfrac{{10\left( {\sqrt 3 + 1} \right)}}{{3 - 1}} \\\ {\text{ = 5}}\left( {2.732} \right) = 13.66m \\\$$

Hence, the height of the building is $13.66m$
Note: In these types of questions it is always necessary to make the figure as described in the question properly as this stage is most prone to error. Then, we use the given angles and lengths and find the desired value using simple trigonometry.