Solveeit Logo
Login

Question

Question: A flag pole 4 m tall casts a 6 m shadow. At the same time, a nearby building casts a shadow of 24 m....

A flag pole 4 m tall casts a 6 m shadow. At the same time, a nearby building casts a shadow of 24 m. How tall is the building?
(a) 12 m
(b) 14 m
(c) 16 m
(d) 17 m

Explanation

Solution

Hint : This problem is related to trigonometry. With the information of the flag pole’s shadow and its height, we find the angle at which the sun is located. Then, once we find the angle, this angle will be the angle of the shadow. Thus, with the length of the shadow, we can find the height of the building.

Complete step-by-step answer :
It is known to us that the height of the flagpole is 4 m and it casts a shadow of length 6 m from its base. To understand this better, we will draw a figure.
Thus, the figure would be as follows:

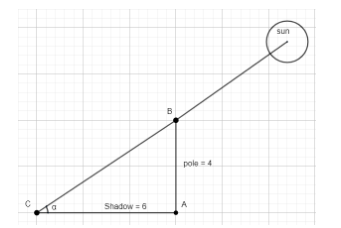
The angle α\alpha is the angle of the orientation of the sun. Since the sun is at an infinite long distance, this angle will be the same for all objects at a given time of the day. Thus, α\alpha for flag post and α\alpha for the building will be the same.
Now, we know that tan⁡θ=oppadj\tan \theta =\dfrac{opp}{adj} . Thus, tan⁡α=heightshadow\tan \alpha =\dfrac{height}{shadow}
Therefore, tan⁡α=46......(1)\tan \alpha =\dfrac{4}{6}......\left( 1 \right)
If α\alpha for flag post and α\alpha for the building will be the same, tan⁡α\tan \alpha for flag post and tan⁡α\tan \alpha for the building will also be the same.
From the given information, we know that the shadow casted by the building is 24 m long from the base of the building.
Thus, we will substitute shadow = 24 in the relation tan⁡α=heightshadow\tan \alpha =\dfrac{height}{shadow}
⇒tan⁡α=height24\Rightarrow \tan \alpha =\dfrac{height}{24}
But from (1), we know that tan⁡α=46\tan \alpha =\dfrac{4}{6}
⇒46=height24\Rightarrow \dfrac{4}{6}=\dfrac{height}{24}
⇒height=4(24)6\Rightarrow height=\dfrac{4\left( 24 \right)}{6}
⇒\Rightarrow height = 16 m
Therefore, the height of the building is 16 m.
So, the correct answer is “Option C”.

Note : It is advisable to draw figures for such types of questions as they can reveal points that can be usually missed. The angle of shadow will change if the time of the day changes, but it will remain the same for all the objects at the same time of the day.