Question

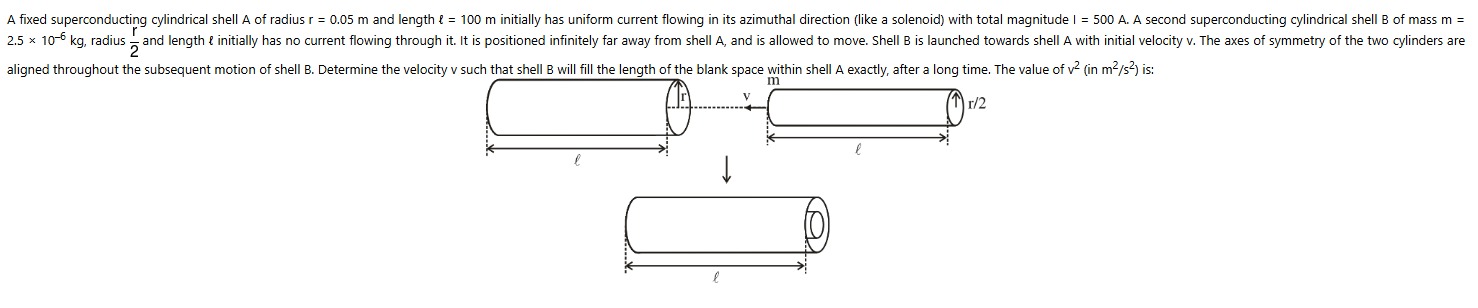
A fixed superconducting cylindrical shell A of radius r = 0.05 m and length $l$ = 100 m initially has uniform current flowing in its azimuthal direction (like a solenoid) with total magnitude I = 500 A. A second superconducting cylindrical shell B of mass m = 2.5 x $10^{-6}$ kg, radius $\frac{r}{2}$ and length $l$ initially has no current flowing through it. It is positioned infinitely far away from shell A, and is allowed to move. Shell B is launched towards shell A with initial velocity v. The axes of symmetry of the two cylinders are aligned throughout the subsequent motion of shell B. Determine the velocity v such that shell B will fill the length of the blank space within shell A exactly, after a long time. The value of $v^2$ (in $m^2/s^2$) is:

Answer 1

3.29

Answer 2

Shell A is a fixed superconducting cylindrical shell with radius $r$ and length $l$, carrying an initial azimuthal current $I$. The magnetic field inside is $B_A = \mu_0 I/l$. The self-inductance is $L_A = \mu_0 \pi r^2/l$. The initial magnetic energy is $U_{initial} = \frac{1}{2} L_A I^2$.

Shell B is a superconducting cylindrical shell with radius $r/2$ and length $l$, mass $m$. Initially, it is at infinity with no current, so its initial kinetic energy is $K_{initial} = \frac{1}{2} m v^2$, and its initial magnetic energy is zero. The initial total energy is $E_{initial} = \frac{1}{2} m v^2 + \frac{1}{2} L_A I^2$.

When shell B is fully inside shell A, let the currents be $I_A'$ and $I_B'$. Due to flux conservation in superconducting shells:

• Initial flux through A: $\Phi_{A,initial} = L_A I$
• Final flux through A: $\Phi_{A,final} = L_A I_A' + M I_B'$

$\Phi_{A,final} = \Phi_{A,initial} \implies L_A I_A' + M I_B' = L_A I$.

• Initial flux through B: $\Phi_{B,initial} = 0$
• Final flux through B: $\Phi_{B,final} = L_B I_B' + M I_A'$

$\Phi_{B,final} = \Phi_{B,initial} \implies L_B I_B' + M I_A' = 0$.

The self-inductance of B is $L_B = \mu_0 \pi (r/2)^2/l = L_A/4$. The mutual inductance when B is inside A is $M = \mu_0 \pi (r/2)^2/l = L_B = L_A/4$.

Substituting $L_B = M = L_A/4$ into the flux conservation equations:

$L_A I_A' + (L_A/4) I_B' = L_A I \implies I_A' + \frac{1}{4} I_B' = I$ (1)

$(L_A/4) I_B' + (L_A/4) I_A' = 0 \implies I_B' + I_A' = 0 \implies I_B' = -I_A'$ (2)

Substitute (2) into (1): $I_A' - \frac{1}{4} I_A' = I \implies \frac{3}{4} I_A' = I \implies I_A' = \frac{4}{3} I$.

Then $I_B' = -\frac{4}{3} I$.

The final state is when shell B is inside A and at rest, so $K_{final} = 0$. The final magnetic energy is:

$U_{final} = \frac{1}{2} L_A (I_A')^2 + \frac{1}{2} L_B (I_B')^2 + M I_A' I_B'$

$U_{final} = \frac{1}{2} L_A (\frac{4}{3} I)^2 + \frac{1}{2} (L_A/4) (-\frac{4}{3} I)^2 + (L_A/4) (\frac{4}{3} I) (-\frac{4}{3} I)$

$U_{final} = \frac{1}{2} L_A \frac{16}{9} I^2 + \frac{1}{8} L_A \frac{16}{9} I^2 - \frac{1}{4} L_A \frac{16}{9} I^2 = \frac{16}{9} L_A I^2 (\frac{1}{2} + \frac{1}{8} - \frac{1}{4}) = \frac{16}{9} L_A I^2 (\frac{4+1-2}{8}) = \frac{16}{9} L_A I^2 \frac{3}{8} = \frac{2}{3} L_A I^2$.

By conservation of energy: $K_{initial} + U_{initial} = K_{final} + U_{final}$.

$\frac{1}{2} m v^2 + \frac{1}{2} L_A I^2 = 0 + \frac{2}{3} L_A I^2$.

$\frac{1}{2} m v^2 = \frac{2}{3} L_A I^2 - \frac{1}{2} L_A I^2 = (\frac{4-3}{6}) L_A I^2 = \frac{1}{6} L_A I^2$.

$v^2 = \frac{1}{3m} L_A I^2 = \frac{1}{3m} (\mu_0 \frac{\pi r^2}{l}) I^2$.

Substitute the given values: $m = 2.5 \times 10^{-6}$ kg, $r = 0.05$ m, $l = 100$ m, $I = 500$ A, $\mu_0 = 4\pi \times 10^{-7}$ T m/A.

$v^2 = \frac{1}{3 \times 2.5 \times 10^{-6}} \times (4\pi \times 10^{-7}) \times \frac{\pi (0.05)^2}{100} \times (500)^2$

$v^2 = \frac{1}{7.5 \times 10^{-6}} \times 4\pi \times 10^{-7} \times \frac{\pi \times 25 \times 10^{-4}}{10^2} \times 25 \times 10^4$

$v^2 = \frac{10^6}{7.5} \times 4\pi \times 10^{-7} \times \pi \times 25 \times 10^{-6} \times 25 \times 10^4$

$v^2 = \frac{4 \times 25 \times 25}{7.5} \times \pi^2 \times 10^{6-7-6+4} = \frac{2500}{7.5} \times \pi^2 \times 10^{-3}$

$v^2 = \frac{1000}{3} \times \pi^2 \times 10^{-3} = \frac{\pi^2}{3}$.

Using $\pi^2 \approx 9.87$: $v^2 \approx \frac{9.87}{3} = 3.29$.