Question

A fixed metallic sheet of width b and a straight wire (in same plane) are carrying same current $I$ in same direction. The force of attraction per unit length on the wire is $\frac{\mu_0I^2}{\alpha \pi b}ln(\frac{a+b}{\beta a})$. Find $(\alpha + \beta)$.

Answer 1

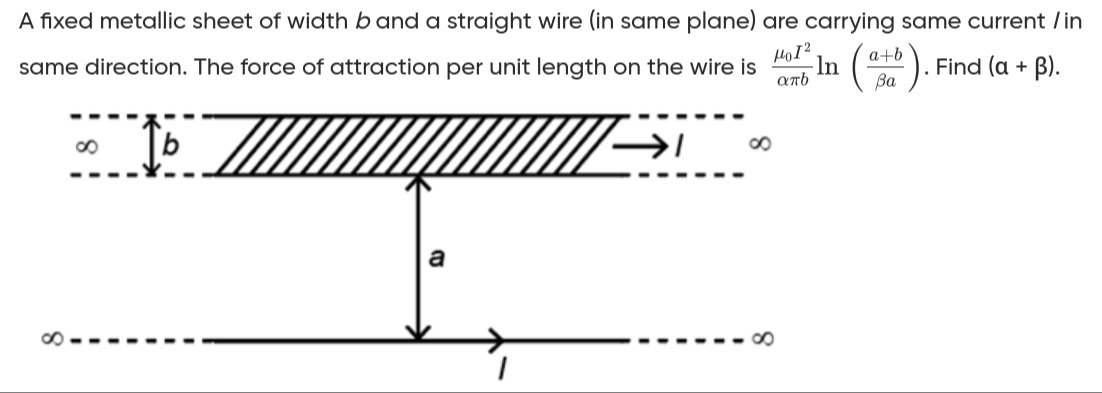
3

Answer 2

To determine the force of attraction per unit length on the wire, we consider the magnetic field produced by the straight wire and the force it exerts on the current-carrying metallic sheet. By Newton's third law, the force on the wire due to the sheet will be equal in magnitude and opposite in direction to the force on the sheet due to the wire. Since the currents are in the same direction, the force is attractive.

1. Magnetic Field due to the Straight Wire:

   Let the straight wire be placed along the x-axis. The current $I$ flows in the positive x-direction. The magnetic field produced by an infinitely long straight wire at a distance $y$ from it is given by:

   $B = \frac{\mu_0 I}{2\pi y}$

   According to the right-hand thumb rule, if the wire is below the sheet and current flows to the right, the magnetic field above the wire (where the sheet is located) points into the page (or in the negative z-direction).

2. Force on an Elemental Strip of the Metallic Sheet:

   The metallic sheet has a width $b$ and carries a total current $I$. We can consider the sheet as being composed of many infinitesimally thin parallel wires.

   Let $J = I/b$ be the current per unit width of the sheet.

   Consider an elemental strip of the sheet of width $dy$ at a distance $y$ from the straight wire. The current in this elemental strip is $dI' = J dy = (I/b) dy$.

   The distance $y$ varies from $a$ (the closest edge of the sheet to the wire) to $a+b$ (the farthest edge of the sheet from the wire).

   The current $dI'$ in this strip also flows in the positive x-direction.

   The force $dF$ on this elemental strip of unit length ($L=1$) due to the magnetic field $B$ from the straight wire is given by:

   $dF = dI' L B \sin\theta$

   Since the current in the strip (x-direction) is perpendicular to the magnetic field (z-direction), $\theta = 90^\circ$, so $\sin\theta = 1$.

   Substituting the expressions for $dI'$ and $B$:

   $dF = \left(\frac{I}{b} dy\right) (1) \left(\frac{\mu_0 I}{2\pi y}\right)$

   $dF = \frac{\mu_0 I^2}{2\pi b} \frac{dy}{y}$

3. Direction of the Force:

   Using Fleming's left-hand rule or the cross product $\vec{F} = I(\vec{L} \times \vec{B})$:

   Current $\vec{L}$ is in $+x$ direction. Magnetic field $\vec{B}$ is in $-z$ direction.

   $\vec{L} \times \vec{B} \propto \hat{i} \times (-\hat{k}) = -(\hat{i} \times \hat{k}) = -(-\hat{j}) = \hat{j}$.

   So, the force on the elemental strip of the sheet is in the positive y-direction, i.e., upwards. This means the force on the sheet is away from the wire (repulsive).

   However, the problem statement explicitly says "force of attraction". This indicates that the currents must be in opposite directions for repulsion, or my interpretation of the diagram (relative direction of current) is incorrect. Let's re-examine the diagram.

   The diagram shows both currents pointing to the right (same direction). For currents in the same direction, the force is always attractive.

   Let's re-evaluate the direction of the magnetic field and force.

   If the straight wire is at $y=0$ (current $I$ in $+x$), and the sheet is at $y \in [a, a+b]$ (current $I$ in $+x$).

   Magnetic field at $y>0$ due to wire is $\vec{B} = \frac{\mu_0 I}{2\pi y} (-\hat{k})$. (Into the page).

   Force on sheet element $dI'$ (in $+x$ direction) is $d\vec{F} = dI' (\hat{i} \times \vec{B}) = dI' (\hat{i} \times \frac{\mu_0 I}{2\pi y} (-\hat{k})) = dI' \frac{\mu_0 I}{2\pi y} (\hat{i} \times (-\hat{k})) = dI' \frac{\mu_0 I}{2\pi y} (\hat{j})$.

   This force is in the $+y$ direction, which means it pushes the sheet away from the wire. This is a repulsive force.

   There must be a misunderstanding of the diagram or a convention.

   Let's assume the standard result: parallel currents attract, anti-parallel currents repel. The problem states "same direction" currents, so the force must be attractive. This implies my calculation of the force direction is incorrect, or the coordinate system choice for $\vec{B}$ is misleading.

   Let's use a simpler approach for direction:

   Current in wire (lower): $I$ (right).

   Current in sheet (upper): $I$ (right).

   Consider a point just above the wire. The magnetic field due to the wire will be into the page.

   Now consider a point below the sheet. The magnetic field due to the sheet will be out of the page.

   The magnetic field at the location of the wire due to the sheet:

   Consider a strip of the sheet. Current $dI'$ to the right.

   Using the right hand rule, the magnetic field produced by this strip at the location of the wire (below it) is out of the page.

   So, the total magnetic field produced by the sheet at the wire's location is $B_{sheet} = \int dB = \int \frac{\mu_0 dI'}{2\pi y}$. This field is out of the page.

   Force on the wire (current $I$ to the right) in a magnetic field (out of the page):

   $\vec{F} = I (\vec{L} \times \vec{B}_{sheet})$. $\vec{L}$ is in $+x$ direction. $\vec{B}_{sheet}$ is in $+z$ direction.

   $\hat{i} \times \hat{k} = -\hat{j}$.

   This means the force on the wire is in the $-y$ direction, which is downwards, towards the sheet. This is an attractive force. This matches the problem statement.

   So, the calculation for the magnitude remains the same, but the interpretation of which object's field acts on which object's current, and the resulting direction, is crucial. My initial calculation of $dF$ was correct in magnitude, and the direction should lead to attraction.

4. Total Force per Unit Length:

   To find the total force per unit length on the wire (which is equal to the total force per unit length on the sheet, by Newton's third law), we integrate $dF$ over the width of the sheet, from $y=a$ to $y=a+b$:

   $\frac{F}{L} = \int_a^{a+b} dF = \int_a^{a+b} \frac{\mu_0 I^2}{2\pi b} \frac{dy}{y}$

   $\frac{F}{L} = \frac{\mu_0 I^2}{2\pi b} \int_a^{a+b} \frac{1}{y} dy$

   $\frac{F}{L} = \frac{\mu_0 I^2}{2\pi b} [\ln y]_a^{a+b}$

   $\frac{F}{L} = \frac{\mu_0 I^2}{2\pi b} (\ln(a+b) - \ln a)$

   Using the logarithm property $\ln P - \ln Q = \ln(P/Q)$:

   $\frac{F}{L} = \frac{\mu_0 I^2}{2\pi b} \ln\left(\frac{a+b}{a}\right)$

5. Comparing with the Given Expression:

   The given force of attraction per unit length on the wire is:

   $\frac{F}{L}_{given} = \frac{\mu_0I^2}{\alpha \pi b}ln\left(\frac{a+b}{\beta a}\right)$

   Comparing our derived expression with the given expression:

   $\frac{\mu_0 I^2}{2\pi b} \ln\left(\frac{a+b}{a}\right) = \frac{\mu_0I^2}{\alpha \pi b}ln\left(\frac{a+b}{\beta a}\right)$

   Equating the coefficients of the logarithm term:

   $\frac{1}{2\pi b} = \frac{1}{\alpha \pi b}$

   $\frac{1}{2} = \frac{1}{\alpha} \implies \alpha = 2$

   Equating the arguments of the logarithm:

   $\frac{a+b}{a} = \frac{a+b}{\beta a}$

   $\frac{1}{a} = \frac{1}{\beta a} \implies \beta = 1$

6. Calculating $(\alpha + \beta)$:

   $(\alpha + \beta) = 2 + 1 = 3$