Question
Question: A fixed mass of gas is taken through a process \( A \to B \to C \to A \) . Here \( A \to B \) is iso...
A fixed mass of gas is taken through a process A→B→C→A . Here A→B is isobaric B→C is adiabatic and C→A is isothermal.
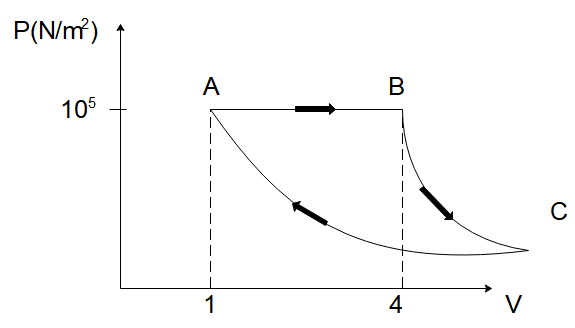
The pressure at C is given by (γ=1.5)
A) 64105N/m2
B) 32105N/m2
C) zero
D) 105N/m2
Solution
To determine the pressure at point C, we will use the properties of the thermodynamic process that can help us relate the pressure and temperature of the gas at a point. The process B→C is adiabatic and we can use the property of adiabatic processes to find the pressure at C.
Formula used: In this solution we will be using the following formula,
For an adiabatic process, PVγ=constant , where P is the pressure of the gas and V is the volume of the gas.
Complete step by step solution:
In the diagram given to us, we have the pressure of the gas on the y -axis and its volume on the y -axis. We’ve been told that the gas undergoes a process A→B→C→A and we want to find out the pressure of the gas in the middle of the process at point C.
We can see that the pressure of the gas at point B is 105N/m2 and the volume of the gas at B is 4m3 . Now the process the gas undergoes from point B to C is adiabatic in nature. Since for an adiabatic process,
PVγ=constant
For the process from B to C, we can write
PBVBγ=PCVCγ
Since PB=105N/m2 , VB=4m3 and (γ=1.5) , we can write
105(4)1.5=PCVCγ
To find the pressure at point C, we need to find the volume of the gas at point C and substitute it in the above equation. To find the volume at C, we will focus on the process C→A . Since it is an isothermal process
PAVA=PCVC
Which we can write as
PCPAVA=VC
On placing the values of pressure and volume at point A, we get
PC105×1=VC
Placing the value of the volume of the gas at point C in equation (1), we get
105(4)1.5=PC(PC105×1)1.5
⇒105(4)1.5=PC(105×1)1.5
Solving for PC in the above equation, we get
⇒PC=1051(4105×1)1.5
Squaring on both sides,
PC=10101(4105×1)3
⇒PC=64105N/m2 which corresponds to option (A).
Note:
While the process of B to C is adiabatic, we don’t know the value of pressure or temperature at C. So, we will have to use the appropriate properties of thermodynamics processes for 2 processes in the system that involve point C that is B→C and C→A .
