Question

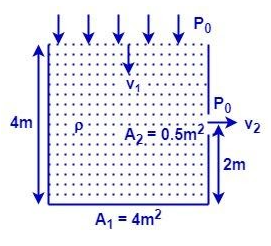
A fixed container is filled with a liquid of density $\rho$up to a height 4m. A horizontal slit of area = 0.5m2 is made of height of 2m from bottom. What is the speed of the top surface of the water level? (Area of top surface of container is 4m2 and g=10m/$s^2$)

A. $\sqrt{\dfrac{20}{63}}m/\sec$
B. $\sqrt{\dfrac{40}{63}}m/\sec$
C. $\sqrt{\dfrac{80}{63}}m/\sec$
D. None of these

Answer 1

Using Bernoulli's equation of top water surface and the slit we can find the velocity of top surface of water level. Bernoulli’s equation is given as:
${{\rho }_{1}}g{{h}_{1}}+\dfrac{1}{2}{{\rho }_{1}}{{v}_{1}}^{2}+{{P}_{1}}={{\rho }_{2}}g{{h}_{2}}+\dfrac{1}{2}{{\rho }_{2}}{{v}_{2}}^{2}+{{P}_{2}}$
Where, ${{\rho }_{1}}\text{ and }{{\rho }_{2}}$are the densities of the two liquids.
${{v}_{1}}\text{ and }{{v}_{2}}$ are the velocities and ${{P}_{1}}\text{ and }{{P}_{2}}$are the two pressures.

Complete step by step solution:

Using the equation of continuity i.e.
${{A}_{1}}{{v}_{1}}={{A}_{2}}{{v}_{2}}$
This is a statement of the principle of mass conservation for a steady, one-dimensional flow, with one inlet and one outlet of areas ${{A}_{1}}\ \text{and }{{A}_{2}}$are the areas of these outlets.
${{v}_{2}}=\dfrac{{{A}_{1}}{{v}_{1}}}{{{A}_{2}}}$
$\begin{aligned} & {{A}_{1}}=4{{m}^{2}} \\\ & {{A}_{2}}=0.5{{m}^{2}} \\\ \end{aligned}$
$\begin{aligned} & {{v}_{2}}=\dfrac{4{{v}_{1}}}{0.5} \\\ & {{v}_{2}}=8{{v}_{1}}\text{ }.....................\text{ (1)} \\\ \end{aligned}$
Now using the Bernoulli’s equation at top water surface and the slit:
${{\rho }_{1}}g{{h}_{1}}+\dfrac{1}{2}{{\rho }_{1}}{{v}_{1}}^{2}+{{P}_{1}}={{\rho }_{2}}g{{h}_{2}}+\dfrac{1}{2}{{\rho }_{2}}{{v}_{2}}^{2}+{{P}_{2}}$
Here, ${{\rho }_{1}}={{\rho }_{2}}=\rho$(as the liquid medium is same i.e. water)
Also ${{P}_{1}}={{P}_{2}}={{P}_{0}}$(the pressure exerted on water surface by the air)
So,
$\begin{aligned} & \rho g{{h}_{1}}+\dfrac{1}{2}\rho {{v}_{1}}^{2}+{{P}_{0}}=\rho g{{h}_{2}}+\dfrac{1}{2}\rho {{v}_{2}}^{2}+{{P}_{0}} \\\ & \rho g{{h}_{1}}+\dfrac{1}{2}\rho {{v}_{1}}^{2}=\rho g{{h}_{2}}+\dfrac{1}{2}\rho {{v}_{2}}^{2} \\\ \end{aligned}$
Here
$\begin{aligned} & {{h}_{1}}=4m\text{ (height of water filled in the container)} \\\ & {{h}_{2}}=2m\text{ (height of the slit from bottom)} \\\ \end{aligned}$
Substituting these values in the above equation and also using equation (1) in here we get;
$\begin{aligned} & \rho g(4)+\dfrac{1}{2}\rho {{v}_{1}}^{2}=\rho g(2)+\dfrac{1}{2}\rho {{(8{{v}_{1}})}^{2}} \\\ & 4\rho g+\dfrac{1}{2}\rho {{v}_{1}}^{2}=2\rho g+\dfrac{1}{2}\rho (64{{v}_{1}}^{2}) \\\ & 4\rho g-2\rho g=\dfrac{1}{2}\rho (64{{v}_{1}}^{2})-\dfrac{1}{2}\rho {{v}_{1}}^{2} \\\ & 2\rho g=\dfrac{1}{2}\rho (63{{v}_{1}}^{2}) \\\ & 4g=63{{v}_{1}}^{2} \\\ & 4(10)=63{{v}_{1}}^{2} \\\ & 40=63{{v}_{1}}^{2} \\\ & {{v}_{1}}^{2}=\dfrac{40}{63} \\\ & {{v}_{1}}=\sqrt{\dfrac{40}{63}}m/\sec \\\ \end{aligned}$
Therefore, option (B) is the correct answer.

Note: Remember that Bernoulli theorem states that the total mechanical energy of the flowing fluid, comprising the energy associated with fluid pressure, the gravitational potential energy of elevation and the kinetic energy of fluid motion, remains constant. Bernoulli's theory is the principle of saving energy for the ideal fluid in a stable, or advanced way and is the basis of many engineering applications. Bernoulli's theory implies that if the fluid flows upwards so that no change in gravitational force occurs, then a decrease in fluid pressure is associated with an increase in velocity fluid. If the fluid flows through a straight pipe of a different cross-sectional area, for example, the fluid accelerates in confined spaces so that the resulting pressure is at least when the cross section is too small. This condition is sometimes called the Venturi effect.