Question
Question: A fish looking up through the water sees the outside world in a circular horizon. If the refractive ...
A fish looking up through the water sees the outside world in a circular horizon. If the refractive index of water is 34 and the fish is 12cm below the surface, the radius of the circle (in cm ) is :
A.365
B.45
C.367
D.736
Solution
Hint: The fish is restricted to see through a circular aperture due to Total Internal reflection. We can find the maximum angle at which a light ray can enter into water and imagine a cone of light rays. The required radius is the radius of the base of this cone, formed at the water-glass interface.
Complete step by step answer:
Let us first see why the fish can only see the world through a circular portion of water.
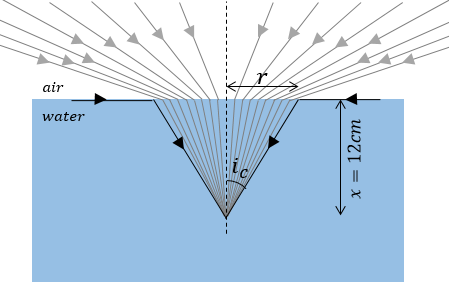
If we imagine light rays coming from the eyes of the fish, then we know that all the rays that hit the water-air interface with an angle lesser than the critical angle would get refracted and reach to the outside world. All the rays with angles greater than the critical angle would be totally internally reflected. Now we know from the principle of reversibility of light that if we reverse the direction of any ray, it would trace back the same path it took. So we can say that all the light coming from the outside world enters the eyes of the fish through a cone. We can see from the diagram that the half-angle of this cone would be the critical angle of the water-air interface.
If we find the critical angle, (which is equal to the half-angle of the cone) then we can easily find the radius of the circle.
We know that a ray coming out of the water at the critical angle would grace the surface of the interface and hence have an angle of refraction of 90o. Let us say this critical angle of incidence is ic. So we can use Snell's law to find the angle of incidence.
sin(90)sinic=nwna=4/31=43.
sinic=43
Now we can see from the diagram that if r is the radius of the circle and x is the depth at which the fish is present, then
r=xtanic
Now, since we know sinic, tanic can be found as :
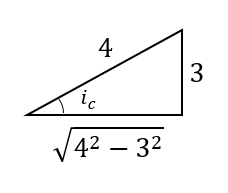
tanic=42−323=73
So the radius would be: r=xtanic=12cm×73=736cm.
Note: Though the fish sees through a small circle, it is seeing the complete outside world. All light striking the air-water interface with angles 0o to 90o gets into water with angle of refraction in between 0o and ic. We can see from the diagram that all rays from the outside are actually coming in. It is just that all of the light gets compressed to fit inside the cone.
