Question

A fish is looking at a 1.0 m high plant at the edge of a pond. Will the planet appear to the fish short?

Answer 1

When the light ray passes through a rare medium to a denser medium, the path of the light bends towards the normal. Draw the ray diagram of the image formation from the fish’s perspective. Extend the refracted ray backwards to find out the size of the planet.

Complete step by step answer:
We know that when the light ray passes through a rare medium to a denser medium, the path of the light bends towards the normal. In this case, the light rays reflected from the top of the plant undergo refraction at the boundary between air and water. Since the water is the denser medium compared to the air medium, the path of the incident ray bends towards the normal and meets at the eye of the fish as shown in the figure below. Let’s extend the ray EM backwards where it meets at point P. The light ray will appear to be reflected from the point P from the fish’s perspective. Therefore, the image of the plant will be PB instead of AB and thus the planet will appear taller.

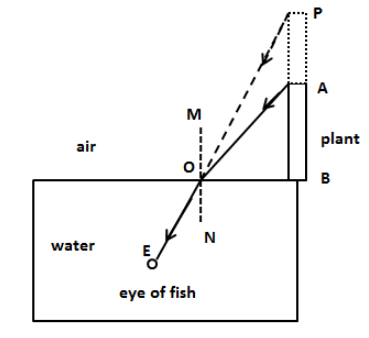
Let the height of the plant is AB which is 1 m. The relation between refractive index, apparent height and real height of the object is,
${\mu _w} = \dfrac{{{h_{app}}}}{{{h_{real}}}}$
$\Rightarrow {h_{app}} = {\mu _w}{h_{real}}$
Substituting 1.3 for ${\mu _w}$ and 1 m for ${h_{real}}$ in the above equation, we get,
${h_{app}} = \left( {1.3} \right)\left( 1 \right)$
$\therefore {h_{app}} = 1.3\,{\text{m}}$

Thus, the plant will appear 1.3 m for the fish.

Note: While drawing the ray diagrams, always check the direction of the incident ray and refracted ray. The incident ray is always reflected from the object towards our eye and not from our eye to the object. While answering these questions, the essential step is to remember the refractive index of the commonly given mediums such as air, liquid or vacuum.